Оценка точности результатов равноточных измерений. Арифметическая середина

Если имеется ряд результатов равноточных измерений l₁; l₂; …; l_n одной и той же величины, то за окончательное значение принимают среднюю арифметическую величину L из всех результатов.

.

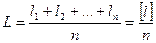Если истинное значение измеряемой величины х, то абсолютные ошибки будут равны:

Δ₁= l₁- х;

Δ₂= l₂- х;

………;

Δ _n= l_n- х,

________

[Δ] = [l] – nx.

Из суммы равенств получим, что .

В соответствии со свойством 4 случайных ошибок, с увеличением числа измерений величина 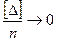при n → ∞.

Следовательно, при бесконечно большом числе измерений, среднее арифметическое L будет стремиться к истинному значению измеряемой величины х.

Величина при конечном числе измерений будет вероятнейшим значением определяемой величины, называемой арифметической серединой. Разность между результатом измерения и средним арифметическим называют уклонением от арифметической середины или вероятнейшими ошибками υ, т. е. l₁ - L = υ₁.

Сумма вероятнейших ошибок равняется нулю 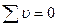, если величина среднего арифметического не имела округлений.

В топографии и геодезии в качестве критериев точности измерений в основном применяют среднюю квадратическую ошибку и относительную ошибку.

Среднюю квадратическую ошибку отдельного результата измерения m вычисляют по формуле Гаусса: .

Формулу Гаусса можно использовать, когда известно истинное значе­ние измеренной величины, а для оценки точности величин, истинное значение которых неизвестно, применяется формула Бесселя 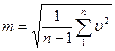, где υ – вероятнейшая ошибка.

Среднюю квадратическую ошибку арифметической середины М выражают через среднюю квадратическую ошибку m отдельного изме­рения, т. е. .

Таким образом, средняя квадратическая ошибка арифметической середины из результатов равноточных измерений в 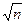раз меньше средней квадратической ошибки результата отдельного измерения. Для уменьшения ошибки измерения, например, в 2 раза, количество измерений необходимо увеличить в 4 раза.

Применительно к конкретным условиям указывают критерий отбра­ковки результатов измерений. В качестве такого критерия служит пре­дельная ошибка. Для наиболее значимых измерений применяются повы­шенные требования к точности и величину предельной ошибки прини­мают равной 2m, т. е. Δ_пр.= 2m (удвоенное значение средней квадратической ошибки. Для менее значимых измерений принимается величина предельной ошибки равная 3m, т. е. Δ_пр.=3m (утроенное значение средней квадратической ошибки).

Пример, если при угловых измерениях m = 5˝, то «по правилу 2m» отбраковываются все результаты, значения которых по абсолютной величине больше 10˝, а применительно к «правилу 3m» отбраковываются – больше 15˝.

Для суждения о точности многих измерений недостаточно определения величины абсолютной ошибки, необходимо еще знать значение самой измеряемой величины. Так, для получения представления о точности линейных, площадных и других измерений применяется относительная ошибка.

Относительная ошибка – это отвлеченное число, выражающее отношение абсолютной ошибки к результату измерения. Относительную ошибку принято выражать простой дробью, числитель которой равен единице.

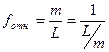– для отдельного результата измерений

–для арифметической середины.

Значение знаменателя принято округлять до двух значимых цифр. Чем больше знаменатель, тем выше точность выполненных работ.

Рассмотрим пример. Измерены две линии: одна длиной 220 м со средней квадратической ошибкой 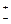0,17 м, другая – длиной 390 м со средней квадратической ошибкой 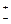0,23 м, т. е. L₁ = 220 м, m₁= 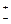0,17 м, L₂ = 390 м, m₂= 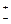0,23 м. Какая из линий измерена точнее?

Подставив результаты измерений и вычислений в вышеприведенные формулы,получим,что относительная ошибка в первом случае будет равна 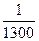, а во втором – . Следовательно, вторая линия измерена точнее, несмотря на большую величину абсолютной ошибки.

4.5. Оценка точности результатов неравноточных
измерений

При неравноточных измерениях нельзя принимать в обработку среднее арифметическое из результата ряда наблюдений, т. к. необходимо учитывать достоверность каждого результата. Более точные измерения должны оказывать большее влияние на окончательный результат.

Для обработки результатов неравноточных измерений вводят понятие о математическом весе измерения. Вес определяет степень надежности результатов измерений. Чем точнее результат измерений, тем больше его вес. Точность результата измерения характеризуется его средней квадратической ошибкой. Следовательно, чем меньше средняя квадратическая ошибка результата измерения и чем больше его вес, тем надежнее результат.

Таким образом, вес результата измерения р – это величина обратно пропорциональная квадрату средней квадратической ошибки, характеризующей результат данного измерения.

Если ряд неравноточных измерений l₁; l₂; …; l_n, а их средние квадратические ошибки имеют значения m₁; m₂; …; m_n, то соответствующие им веса, будут 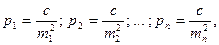где с – некоторая постоянная величина, число произвольное, но одно и тоже при определении значений всех весов.

Обозначим вес среднего арифметического, полученного из n измерений Р, а вес одного измерения – p, тогда

Следовательно, вес арифметической середины в n раз больше веса каждого отдельного результата измерения.

Пусть некоторая величина Х измерена n раз в различных условиях. При этом получены результаты l₁ с весом p₁ , l₂ с весом p₂, и т. д. соответственно. Тогда наиболее вероятным значением будет среднее весовое или общее арифметическое среднее (общая арифметическая середина), вычисляемое по формуле .

Общей арифметической серединой или весовым средним неравноточных измерений называется сумма произведений результата каждого измерения на его вес, разделенная на сумму весов.

Истинные значения измеряемых величин, как правило, неизвестны, поэтому при оценке точности результатов неравноточных измерений используют вероятнейшие ошибки.

Средняя квадратическая ошибка единицы веса µ определяется по формуле 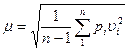, где υ – вероятнейшая ошибка (уклонение от общей арифметической середины) υ = l – L₀ ; n – число измерений.

Средняя квадратическая ошибка весового среднего или общей арифметической средней М₀ вычисляется по формуле 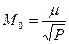, где Р – сумма весов.