Свойства случайных ошибок
Если одну и ту же величину, истинное значение х которой известно, многократно определить с равной точностью, то получим ряд измерений l1, l2, … ln. Каждое измерение будет иметь свою случайную ошибку Δ1, Δ2, … Δn, т. е. l1- х = Δ1; l2- х = Δ2; …; ln- х = Δn.
Полученный ряд случайных ошибок обладает определенными статистическими свойствами:
1. Свойство симметричности, т. е. равные по абсолютной величине, но разные по знаку ошибки встречаются в рядах результатов измерений одинаково часто.
2. Свойство унимодальности или сосредоточения, т. е. малые по абсолютному значению ошибки встречаются чаще чем большие.
3. Свойство ограниченности, т. е. абсолютное значение случайных ошибок результатов измерений не может быть больше некоторого известного предела (предельной погрешности) Δi £ Δ пред. Величина предельной погрешности устанавливается инструментами.
4. Свойство компенсации, т. е. среднее арифметическое из всех случайных ошибок ряда измерений при неограниченном увеличении числа измерений, стремится к нулю  , где Δ – случайные ошибки, n – количество измерений.
, где Δ – случайные ошибки, n – количество измерений.
Если суммы обозначить квадратными скобками [ ] (символ сумм Гаусса), то можно записать 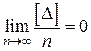 .
.

 Если на оси ординат (рис. 4.1) отложить величины случайных ошибок, а на оси абсцисс – число ошибок ряда измерений и через полученные точки провести кривую линию, то получим график распределения случайных ошибок, который характеризует указанные свойства. Из графика случайных ошибок следует, что большее число случайных ошибок расположено в пределах их значений от –1 до +1.
Если на оси ординат (рис. 4.1) отложить величины случайных ошибок, а на оси абсцисс – число ошибок ряда измерений и через полученные точки провести кривую линию, то получим график распределения случайных ошибок, который характеризует указанные свойства. Из графика случайных ошибок следует, что большее число случайных ошибок расположено в пределах их значений от –1 до +1.
Приведем пример, подтверждающий свойства случайных ошибок. В результате 10-кратного измерения расстояния мерной лентой получили следующие случайные ошибки (табл. 4.1).
Таблица 4.1
| Измерения | ||||||||||
| Ошибки, см | -1 | +2 | -1 | +1 | +2 | -2 | -3 | +4 | -1 | +6 |
Из данного ряда результатов измерений можно отметить, что ошибок по абсолютному значению от 0 до 2 см – семь, от 3 до 4 см – две, свыше 4 см – одна. Среднее арифметическое из десяти ошибок равняется 0,7 см.
Дата добавления: 2015-06-27; просмотров: 2146;
