Проекции топографических карт. Зональная система плоских прямоугольных координат

На выбор картографических проекций влияют многие факторы. Для топографических карт важнейшим требованием является минимальность искажений, и в первую очередь, линейных, то есть сохранение масштаба длин по всей карте. Поскольку топографические карты широко используются для определения ориентирующих углов, то необходимым условием является сохранение по всей карте равноугольного изображения. Для уменьшения линейных искажений земной эллипсоид делится на части – геодезические зоны, которые образованы меридианами через 6º по долготе, начиная от Гринвичского. Число зон составляет 60 и нумерация их ведется к востоку.

На территории Республики Беларусь и других стран СНГ все топографические карты составляются в равноугольной проекции Гаусса-Крюгера. Немецкий ученый К. Ф. Гаусс в 1825–1830 гг. для обработки Ганноверской триангуляции применил разработанную им равноугольную проекцию. Детальный вывод рабочих формул этой проекции в 1912 г. выполнил немецкий геодезист Л. И. Крюгер. Поэтому она получила название Гаусса-Крюгера и ее вычисляют аналитически.

С методической точки зрения получение этой проекции можно условно представить следующим образом. Для этого поместим земной шар в цилиндр так, чтобы ось вращения его была перпендикулярна оси цилиндра РР₁, а линия касания являлась меридианом NOS (рис. 3.1), который примем за осевой (средний) меридиан геодезической зоны. Он изобразится на цилиндрической поверхности в виде прямой без изменения длины. Остальная поверхность геодезической зоны (например, NFSD) проецируется на поверхность цилиндра так, чтобы каждая бесконечно малая фигура, например, окружность, сохранила свою форму, изменяя только радиус.

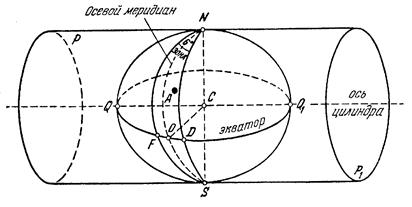
Рис. 3.1

В проекции Гаусса–Крюгера картографическая сетка по изображению меридианов и параллелей подобна картографической сетке поперечно-цилиндрической проекции: осевой меридиан и экватор являются прямыми, другие меридианы и параллели – кривыми линиями, пересекающимися под прямым углом.

Масштаб в проекции Гаусса–Крюгера сохраняется по осевому меридиану геодезической зоны. По мере удаления от него длины линий искажаются в сторону увеличения. Поправки Δ S можно вычислить по приблизительной формуле

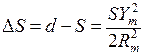, (3.1)

где d и S – соответственно длины линий на плоскости и сфероиде;

Y_m – средняя ордината линии; R_m – средний радиус кривизны сфероида.

Относительное искажение длин линий будет определяться по формуле: f_s = 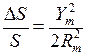и достигнет для средних широт на краю геодезической зоны значения f_s .

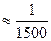Каждая из 60 зон изображается на плоскости независимо от остальных зон и имеет самостоятельную систему прямоугольных координат. Начало координат находится в точке пересечения экватора с осевым меридианом зоны. Положение точки на плоскости определяется плоскими прямоугольными координатами Х и У.

В каждой зоне координаты Х и У могут иметь положительные и отрицательные значения. Положительное значение имеют абсциссы, располагающиеся к северу от экватора, а отрицательное – к югу от экватора. Ординаты (в каждой зоне), отсчитываемые от осевого меридиана к востоку являются положительными, а к западу – отрицательными. В данной системе координат абсциссы всех точек расположенных на территории Республики Беларусь в каждой зоне имеют положительные значения. Во избежание отрицательного значения ординат и для удобства их вычисления, к началу ординат каждой геодезической зоны добавляют 500 км, т. е. начало координат будет: Х₀ = 0; У₀ = 500 км. Тогда ординаты, расположенные к западу от осевого меридиана будут иметь значения меньше 500 км, а расположенные к востоку – значения больше 500 км. Такие ординаты называются преобразованными. Чтобы определить в какой зоне находится данная точка, впереди преобразованной ординаты указывается номер зоны.

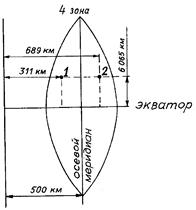
Например, согласно рис. 3.2 точка 2 имеет орди­нату у₂ = 4689 км. Следовательно, она расположена в четвертой зоне на расстоянии 189 км к востоку от осевого меридиана зоны (689–500 = 189). Точка 1 имеет ординату у₁ = 4311 км и находится в этой же зоне на расстоянии 189 км к западу от осевого меридиана зоны (311–500 = –189). Вычисленные плоские прямоугольные координаты в проекции Гаусса-Крюгера для эллипсоида Красовского получили название «Система координат 1942 года» или СК–42.

Масштабы планов и карт

Масштабом плана называется отношение длины линии на плане к соответствующей длине горизонтального проложения этой линии на местности.

Как известно, планы составляются для небольших по площади территорий и поэтому их масштаб можно считать величиной постоянной. На картах следует учитывать искажения длины линий из-за кривизны Земли. Например, для проекции Гаусса–Крюгера поправки вычисляются по формуле 3.1. и при необходимости вводятся в измеренные линии.

Масштаб на планах и картах выражается в численной, именованной и графической формах.

Численный масштаб выражается простой дробью, в числителе которой единица, а в знаменателе число, показывающее во сколько раз горизонтальное проложение линии местности уменьшено при нанесении на план (карту). Масштабы могут быть любыми. Но чаще используются их стандартные величины: 1:500; 1:1000; 1:2000; 1:5000; 1:10 000; 1:25 000; 1:50 000; 1:100 000; 1:200 000; 1:300 000; 1:500 000; 1:1000 000. Например, масштаб карты 1:10 000 указывает, что горизонтальное проложение линии уменьшено на карте в 10 000 раз, т. е. 1 см на плане соответствует 10 000 см на горизонтальной проекции местности. Чем меньше знаменатель численного масштаба, тем крупнее считается масштаб, и наоборот. Численный масштаб величина безразмерная; она не зависит от системы линейных мер, т. е. им можно пользоваться, проводя измерения в любых линейных мерах.

Именованный масштаб представляет краткое словесное выражение численного масштаба и указывает, какая величина горизонтального проложения местности соответствует 1 см на плане (карте). Например, «в 1 сантиметре 100 метров».

Линейный масштаб представ­ляет собой графическое выражение численного и именованного масшта­бов в виде линии, разделенной на равные отрезки – основания. Левый из них ab делится на 10 равных частей (десятые доли). Сотые доли оцениваются «на глаз». На рис. 3.3 показан линейный масштаб с основанием ab = bc = cd…, соответствующий численному масштабу 1:10 000.

Основание линейного масштаба выбирается таким образом, чтобы выражало целое число метров горизонтального проложения линии. В нашем примере оно равно 1 см.

Для более точного измерения линий на плане или карте пользуются поперечным масштабом (рис. 3.4). Для построения поперечного масштаба, на прямой МЕ откладывают отрезки AM = AB = BC = CD = DE, принимаемые за основание масштаба. В точках М, А, В,…, Е восстанавливают перпендикуляры и на крайние из них наносят 10 равных между собой отрезков Ме = Ее = еf = …. Через полученные точки е, f, p, g проводят прямые, параллельные МЕ. Нижнее и верхнее основание масштаба МА и NQ разбивают на 10 равных частей. Точки деления соединяют между собой параллельными наклонными линиями в следующем порядке: точку А с точкой Р, точку N с точкой F и так далее.

Рис. 3.4

Прямая АР и параллельные ей линии называются трансверсалями. Отрезок аb называют наименьшим делением поперечного масштаба. По построению малые отрезки АН, МF, PQ и др. будут равны 0,1 основания масштаба МА, а наименьшее деление аb будет равно 0,1 отрезков АН, МF, PQ и т. д. или 0,01 основания масштаба МА.

Пример: По поперечному масштабу с основанием равным 2 см определим расстояние О'К (рис. 3.4). При численном масштабе 1:10000 основанию в 2 см на плане будет соответствовать 200 м на местности, малые отрезки будут равны 20 м, а наименьшие – 2 м. Таким образом, ОК = 200 м × × 2 = 400 м; малых делений – 5, тогда AG = 20 м × 5 = 100 м и измеряемая линия О'К находится на шестой горизонтальной линии, т. е., 2 м × 6 = = 12 м. Таким образом, измеряемая линия О'К равняется 512 м.

При измерениях длины линий на картах, измеряемая линия берется в раствор циркуля-измерителя и переносится на поперечный масштаб. Необходимо, чтобы правая ножка измерителя находилась на одном из перпендикуляров (справа от основания МА), а левая – на пересечении трансверсали и горизонтальной линии основания МА, при этом обе ножки измерителя должны располагаться на одной горизонтальной линии О'К. Пользуясь поперечным масштабом измеряют длины прямых линий.

Измерение кривых линийпроизводится двумя способами: при помощи курвиметра и циркулем-измерителем.

При первом способе колесико курвиметра прокатывают по измеряемой линии на карте. Стрелка прибора показывает отмеренное колесиком расстояние в сантиметрах (или дюймах). Пользуясь масштабом, определяют расстояние на местности. При измерении длин сильно извилистых линий сложно точно вести колесико по мелким изгибам, в связи с этим точность измерений курвиметром невысока.

При измерении длины кривых линий более точные результаты получают пользуясь вторым способом – применяя циркуль-измеритель с микрометренным винтом. Измерения выполняют малыми растворами измерителя (1–4 мм). Перед измерениями определяют цену раствора измерителя, т. е. измеряют линию, длина которой известна (обычно расстояние между километровыми сетками).

Точность масштаба. Предельные размеры предметов, которые можно различать на плане (карте) определяются графической точностью масштаба. Свойство человеческого зрения позволяет различать точку величиной порядка 0,1 мм. Это связано с критическим углом человеческого зрения, равным 1'. Поэтому расстояние на местности, соответствующее 0,1 мм плана, называют предельной точностью масштаба и ее величина t в метрах зависит от масштаба карты, т. е. t = 0,0001 М, где М – знаменатель масштаба карты. Например, для карты масштаба 1:10 000 предельная точность равна t = 0,0001 ´ 10 000 = 1м, а для карты масштаба 1: 50 000 – t = = 5м. Практически средняя ошибка измерения длин линий на карте составляет 0,3–0,4мм или 0,0003–0,0004 М.