Гравітаційне поле Землі

ГРАВІТАЦІЙНА РОЗВІДКА

Гравітаційна розвідка вивчає поле прискорення сили тяжіння для вирішення геологічних задач.

Силою тяжіння (G) називається сила, з якою тіла притягаються до Землі. Вона є рівнодіючої двох сил: сили притягування F і відцентрової сили Р (рис. 1.1).

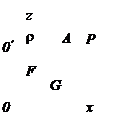
Рисунок 1.1 Вектор сили притягування та його складові

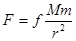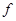Сила притягування Землею тіла масою m підпорядковується закону Ньютона: , де М – маса Землі; - відстань між центрами мас; - гравітаційна постійна ( ).

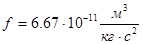Відцентрова сила знаходиться в площині, перпендикулярній до вісі обертання (Z) Землі: 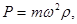де 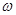- кутова швидкість обертання; 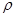- відстань від точки обертання до вісі (АО). Таким чином, сила тяжіння . Мірою сили тяжіння є сила, діюча на одиничну масу. Вона чисельно дорівнює прискоренню сили тяжіння і тому спрощено остання називається силою тяжіння. Ця величина є головною характеристикою гравітаційного поля.

В системі СІ за одиницю прискорення сили тяжіння прийнято прискорення, яке розвиває тіло масою в 1 кг під дією сили в 1 Н. Одиниця її виміру – 1 м/с².

Величина відцентрової сили P змінюється від 0 на полюсах до максимуму на екваторі (0,34 м/с²). Тому сила тяжіння визначається, головним чином, силою притягування F, оскільки відношення . Оскільки відцентрове прискорення мале порівняно з прискоренням сили тяжіння, можна вважати, що .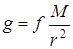

Земля, в першому наближенні, є еліпсоїдом обертання. Її екваторіальний радіус а=6378 км, а полярний – с=6357 км. Різниця а–с=21 км. Різна величина радіусів, з урахуванням зміни величини відцентрової сили на полюсі та екваторі призводить і до змін напруженості гравітаційного поля від 9,78 м/с² на екваторі до 9,83 м/с² на полюсах, тобто сила тяжіння зростає від екватора до полюсів на 5·10^-5 м/с² на 1 км.

Гравітаційне поле відзначається властивостями потенціального поля. Сила тяжіння є векторною величиною. Але поле прискорення сили тяжіння зручніше розглядати, якщо воно представлено скалярними величинами. За скалярну функцію поля приймається функція W, яка називається потенціалом сили тяжіння. З фізичної точки зору він характеризує енергію, яку потрібно витратити, щоб перемістити в полі сили тяжіння тіло одиничної маси із точки спостереження у нескінченність. Потенціал має максимальне значення в центрі Землі і неперервно спадає по мірі віддалення від нього.

Потенціал сили тяжіння для точки, розташованої на поверхні Землі, має вигляд: .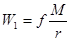

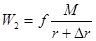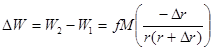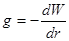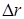У будь-якій іншій точці, розташованій на продовженні земного радіусу r, потенціал дорівнює: . Звідси . В межах, при малому . Звідси , тобто сила ваги являє собою першу похідну потенціалу сили тяжіння в напрямку до центра Землі. Фізичним змістом збільшення потенціалу є робота, що витрачається при русі точкової маси, що притягається на відрізку . Оскільки напрямки і сили g можуть не збігатися, то . При переміщенні точки перпендикулярно до діючої сили, коли кут 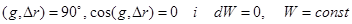. Це рівняння деякої поверхні, у будь-якій точці якої сила тяжіння спрямована по нормалі до неї. Надаючи функції W різні значення, одержимо родину еквіпотенціальних поверхонь, тобто поверхонь рівного потенціалу, що у гравіметрії називають еквіпотенційними поверхнями. Однією з них є поверхня, що збігається з рівнем води у Світовому океані в спокійному стані, яка названа геоїдом. Вона характеризує фігуру Землі.

Якщо прямокутну систему координат розташувати так, щоб початок її координат збігся з точкою дотикання еквіпотенційної поверхні і горизонтальною площиною, вісь х направити на північ, у — на схід, z - перпендикулярно еквіпотенційній поверхні, то 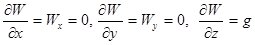, тобто градієнт потенціалу по осі z дорівнює прискоренню сили тяжіння.

У гравіметрії іноді вивчаються також другі похідні гравітаційного потенціалу, а також їхні зміни по осях х і у чи градієнти напруженості по цих осях:

.

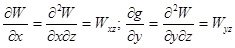Вони називаються горизонтальними градієнтами і характеризують швидкість зміни сили тяжіння в горизонтальній площині. Похідна сили тяжіння у вертикальній площині 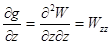називається вертикальним градієнтом напруженості поля. Поряд з цим вимірюються також величини

,

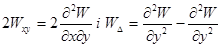які називаються кривизнами. Провівши ряд вертикальних площин (нормальних перетинів) через вісь z (яка є нормаллю до еквіпотенційної поверхні), можна виділити серед них два головних перетини, що мають у даній точці максимальну і мінімальну кривизну (кривизна зворотна радіусу Землі). Зміни потенціалу сили тяжіння в цих площинах будуть зв'язані з кривизнами наступними співвідношеннями: де r₁ і r₂ — менший і більший радіуси Землі, 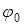— азимут площини нормального перетину з найбільшою кривизною.

Перетин з мінімальною кривизною буде розташовано в азимуті 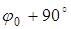геоїда. Як уже зазначалося, під геоїдом розуміється еквіпотенційна поверхня, що збігається з рівнем Світового океану в спокійному стані і екстраполюється під континенти так, що усюди перпендикулярна напрямку повного вектора напруженості гравітаційного поля. Ця поверхня використовується для відліку висот фізичної поверхні Землі. Так, для колишнього Радянського Союзу за початок висот прийнятий середній рівень Балтійського моря. Використання геоїда дозволяє приводити до одного рівня гравітаційні зйомки, виконані на різних висотах. Одиницею виміру других похідних сили тяжіння є секунда в мінус другому степені (с^-2).

Для виділення аномалій сили тяжіння чи її похідних за допомогою гравірозвідки потрібно знання нормальних значень цих величин у даних точках. Під нормальним полем Землі розуміють теоретично розраховане поле в припущенні, що Земля являє собою геометрично правильне тіло, яке складається з однорідних по густині концентричних шарів.

Для обчислення нормальних значень сили тяжіння Землі використовують різні формули, розраховані, як правило, для еліпсоїда обертання.

Приблизно значення нормальної сили тяжіння ( 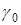) можна оцінити по спрощеній формулі, відомій як запис теореми Клеро: 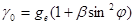, де g_e - середнє значення сили тяжіння на екваторі; 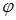- широта пункту спостереження; β = 0,0086692 - α; α - стиснення еліпсоїда обертання 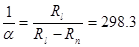, де R_l і R_n - екваторіальний і полярний а радіуси Землі.

При гравітаційних зйомках усі значення сили тяжіння приводяться до єдиного рівня Потсдамської обсерваторії (ФРН).

В інструкції з гравірозвідки (1975 р.) для визначення нормальних значень сили тяжіння передбачена наступна формула: g₀=9,78049 (1+0,005302 sin² φ—0,000007 sin² 2φ)-14×10^-5 м/с².