Упругие волны в изотропных неоднородных средах

Простейшим случаем неоднородной является среда, состоящая из двух различных однородных упругих полупространств, разделенных плоской поверхностью. Обозна- чим скорости и плотности в верхней и нижней средах соответственно через vP1, vS1, ρ1, и vP2, vS2, ρ2. Примем, что поверхность раздела — горизонтальная плоскость. Точечный источник возбуждения расположим в верхней среде на высоте hИ от границы раздела двух полупространств. Поскольку продольные и поперечные волны распространяются с различными скоростями, можно решать задачу для одного типа волн, используя ре- зультаты, независимые от типа возмущения, для другого типа волн. Для определенно- сти примем, что источник возбуждает только продольные волны.

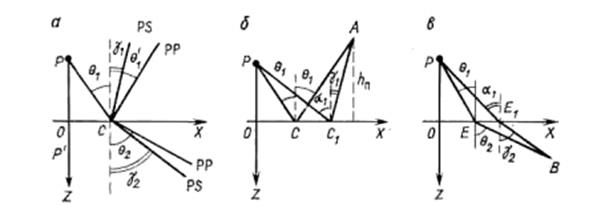
Рис.1.5 Образование отраженных, проходящих и обменных волн на границе двух твердых сред

В силу осевой симметрии задачи относительно вертикальной линии РР' (рис. 1.5) ограничимся рассмотрением только в плоскости XOZ. Расположим точку наблюдения А на высоте hП от границы полупространства. Координаты источника при этом будут xИ=0, zИ=hИ, точки приема — xП=x, zП=hП. За начало отсчета времени будем прини- мать момент возбуждения. Так как каждое из полупространств однородно, возмущение от источника (точки Р) до точки А будет распространяться прямолинейно, по пути РА. Волна, распространяющаяся этим путем, никак не «чувствует» границу раздела, ведет себя так, как если бы все полупространство было неограниченным и снизу. Луч РА на- зывают лучом прямой волны. В точку границы раздела С возмущение также подходит по прямой, отрезку PC. Луч PC называют лучом падающей волны. Направление рас- пространения падающей волны в точке С однозначно определяется углом между лучем

PC и нормалью п к границе в точке С — углом падения θ1. Плоскость, в которой лежит луч падающей волны и нормаль к границе, называют плоскостью падения волны.

Опыт показывает, что звук от источника в точке Р слышен дважды. Второй звук, приходящий позже первого, — это знакомое всем эхо. Появление эха означает, что, дойдя до границы, волна изменяет направление распространения. Но так как и в ниж- ней среде слышен звук, то, следовательно, часть энергии, заключенной в падающей волне, проходит в нижнюю среду под границу, а другая часть отражается. Отражение и проникновение волны происходит в точке С, которую называют поэтому точкой отра- жения для отраженной волны и точкой преломления для проходящей волны. Волну, проходящую в нижнее полупространство, называют преломленной, проходящей.

Распространение двух новых волн подчиняется всем закономерностям, свойст- венным волнам в безграничной среде. Прежде всего, кинематика их должна опреде- ляться лучами (направлениями распространения) и формой фронтов. Источником же волн, распространяющихся вверх от границ и вниз, можно считать те фиктивные ис- точники, которые, согласно принципу Гюйгенса, образуются на границе в момент дос- тижения ее падающей волной. Для того, чтобы определить, каким путем идут отражен- ная и проходящая волны от источника к границе и далее к точке наблюдения в верхнем или нижнем полупространстве, достаточно воспользоваться принципом Ферма. Прин- цип Ферма в данной ситуации приводит к законам Снеллиуса, установленным перво- начально для света. Закон Снеллиуса утверждает, что луч отраженной волны лежит в плоскости падения, направлен вверх от границы, и угол θ1` между этим лучом и норма- лью (угол отражения) всегда равен углу падения, т. е. θ1`=θ1 (рис. 1.5, а). Луч же про- ходящей волны исходит из точки С (точки падения) и лежит в плоскости падения, и угол между нормалью и этим углом (угол преломления) θ2 подчиняется соотношению:

vP 2

sinq2

=

vP1

×sinq 1

(1.11)

Луч PC при продолжении его в нижнюю среду преломился, скачком изменил свое направление.

В жидкостях и газах частицы могут свободно перемещаться вдоль границы разде- ла двух полупространств. Два твердых полупространства контактируют друг с другом так, что при малых деформациях скольжение частиц одного полупространства по гра- нице другого невозможно, частицы на границе находятся в сцеплении друг с другом. Это обстоятельство обусловливает появление в точке С не только отраженной про- дольной волны, одноименной с падающей, но и поперечной SV-волны, которую в этом случае называют обменной отраженной волной. Поперечная PS-волна образуется и в нижнем полупространстве, ее называют обменной проходящей волной. Таким обра- зом, одна падающая продольная волна при встрече на своем пути границы, на которой скачком изменяется скорость продольных волн, порождает четыре волны — две про- дольные и две поперечные. Поперечная падающая волна в общем случае также породит четыре волны — две поперечные и две обменные продольные. Этим звуковые волны существенно отличаются от упругих — в жидкостях и газах граница раздела двух сред порождает только две продольные волны—отраженную и проходящую.

Кинематика обменных волн также вытекает из принципа Ферма и подчиняется обобщенному закону Снеллиуса для упругих волн: лучи этих волн лежат в плоскости падения, а углы отражения γ1 и преломления γ2 обменных поперечных волн (углы меж- ду лучом каждой из этих волн и нормалью к границе в точке падения или отражения) подчиняются соотношениям

vS 1

vP1

sinq1 ,

sing

=vS 2

P1

sinq1

(1.12)

С учетом формулы (1.12) можно записать обобщенный закон Снеллиуса в виде

sin

sin

sing

sing

q1=q2= 1 = 2

(1.13)

vP1

vP 2

vS1

vS 2

где θ1 —угол падения продольной волны; θ2 —угол ее преломления; γ1 и γ2—углы отражения и преломления обменных волн соответственно. Фактически же γ1 и γ2 —это углы, под которыми из точки отражения выходят лучи новых волн, образующихся здесь же на границе.

Принципы Ферма, Гюйгенса и вытекающие из них законы Снеллиуса являются законами геометрической сейсмики. Их использование позволяет решать разнообраз- ные кинематические задачи сейсморазведки.

В точке наблюдения А должно наблюдаться появление трех волн: прямой, идущей по пути РА; продольной отраженной, идущей по пути РСА, так, чтобы θ1=θ1`, и об- менной отраженной (рис. 1.5, б). Она может попасть в точку A, если обменная волна образуется не в точке С, а в точке C1, где угол γ1 связан с углом α1 законом Снеллиуса:

sing

=vS1

P1

(1.14)

В точке B под границей можно наблюдать две волны — продольную и попереч-

ную (рис.1.5, в). Продольная волна идет от источника по пути РЕВ, а обменная волна

— по пути РЕ1В так, что углы θ1, θ2, γ1, γ2 удовлетворяют закону Снеллиуса:

vS 2

vP

sin a1 ;

sin q2 =

vP 2

vP

sin q1 . (1.15)

1 1

Образование головных волн. Как следует из выражения (1.11), если vP2>vP1, то луч преломленной волны по мере увеличения угла падения падающей волны будет приближаться к границе раздела, т. е. sin θ2 > sin θ1. Когда (vP2 ·sin θ1) / vP1= 1, θ2=900, луч преломленной волны направлен строго вдоль границы раздела двух сред (рис. 1.6). Фронт преломленной волны в точках границы оказывается направленным перпендику- лярно к границе, он опирается на нее и в таком положении скользит вдоль границы. Следовательно, энергия к точкам границы, расположенным правее точки K1 и левее

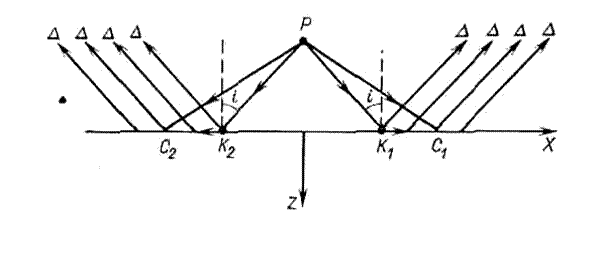Рис.1.6. Образование головных волн

точки K2, поступает двумя путями: непосредственно по прямым PC (см. рис. 1.6) и от источника до точек К1, К2, а затем от этих точек по прямым КС. Поскольку vP2>vP1, волна, идущая по пути РК1С1 (РК2С2), опережает волну, идущую по пути PC. Соглас- но принципу Гюйгенса, точки фронта преломленной волны, расположенные на самой границе, являются источниками, возбуждающими волну иным способом, чем это про- исходило при отражении. Отраженная волна в точке С образуется лишь тогда, когда до нее дойдет падающая, т. е. позже. С помощью принципа Ферма или принципа Гюйгенса устанавливается, что образуемая новым способом волна распространяется только в об- ласти, лежащей правее критического луча К1 (левее K2), лучи этой волны параллельны друг другу и направлены под критическим углом i к нормали к границе так, что

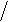sin i

=vP1

vP 2

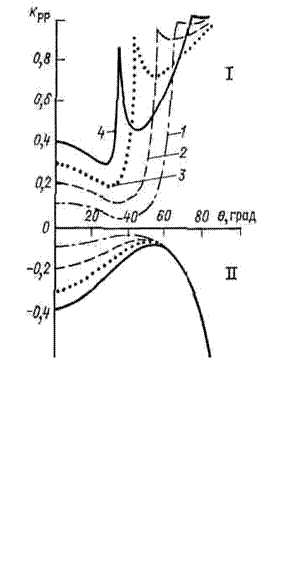Рис.1.7 Зависимость коэффициента отра- жения продольных волн от угла падения.

I — волна падает из среды с параметрами

Новую волну называют головной, и она распространяется по сложной траектории

— от источника до границы по лучу, на- правленному под критическим углом, со скоростью vP1, далее вдоль границы со ско- ростью vP2, и от каждой точки границы по лучу, направленному под тем же критиче- ским углом, со скоростью vP1 она выходит к точкам наблюдения. Если vS2>vP1, то об- разуется и обменная головная волна, иду- щая по лучу, направленному под углом iS в верхней среде как продольная sin iS=vP1/vS2, затем вдоль границы как попе- речная и от границы как поперечная же вверх, по лучу, направленному под тем же углом iS.

Динамика отраженных и головных волн. При падении на плоскую границу раздела продольной сферической волны часть энергии проходит в нижнюю среду, часть —отражается. В твердых средах

Vp=2400 м/с, VS =1440 м/с, ρ =2,2 г/см

на гра-

энергия падающей волны расходуется на

параметрами Vp =2400 м/с, VS =1440 м/с, ρ =

2,2 г/см3 из сред 1—4

образование двух отраженных и двух про- ходящих преломленных волн. Вследствие этого амплитуда колебаний в отраженных волнах должна изменяться относительно амплитуды падающей волны. Динамиче- ская теория упругих волн показывает, что при отражении упругих волн форма им-

пульса отраженной волны совпадает с формой импульса падающей до тех пор, пока угол падения не достигнет критического значения. При дальнейшем увеличении угла падения форма импульса отраженной волны начинает зависеть от угла падения.

Амплитуда отраженной волны определяется двумя факторами — расстоянием, которое волна проходит от источника до границы и далее до точки наблюдения, и ко- эффициентом отражения k(θ) — величиной, не превышающей единицы и зависящей от угла падения и упругих свойств контактирующих сред:

АMAX ОТР =

А0

R1 +R2

×k1 2 (q)

(1.16)

где R1 — расстояние от источника до точки отражения; R2 — расстояние от точки отра- жения до точки наблюдения; A0 — константа, определяющая интенсивность источника; θ — угол падения. Принято, что R1, R2 >> λН, где λН — максимальная длина волны в спектре импульса смещения.

При нормальном падении, когда θ=0, выражение для k1 2 принимает простой вид:

k1 2

=s2 ×v2 -s1 v1,

s 1 ×v1 +s 2 v2

k2 1

=s1 ×v1 -s2 v2.

s 1 ×v1 +s 2 v2

(1.17)

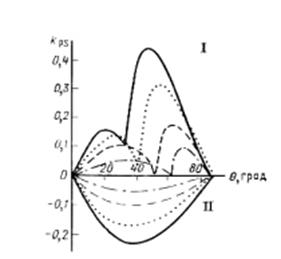
Рис.1.8 Зависимость коэффициента от- ражения обменных волн от угла падения (условные обозначения и параметры сред см. рис.1.7)

Величину Z=σ·v называют акустиче- ской жесткостью для продольных или попе- речных волн соответственно. Как видно из выражений (1.17), отражательная способ- ность границы зависит только от перепада акустических жесткостей, а не просто скоро- стей. При Z1<Z2 коэффициент отражения становится отрицательным. Это означает, что импульсы падающей и отраженной волн соотносятся между собой как зеркально пе- ревернутые относительно оси времени. Та- кой эффект называют обращением полярно- сти — импульс отраженной волны приобре- тает отрицательную полярность относитель- но импульса падающей. Зависимость коэф- фициента отражения от угла падения при различных параметрах упругих сред приве- дена на рис. 1.7. При углах падения, не пре- вышающих критического значения, импуль- сы обменных волн имеют ту же форму, что и импульсы падающих. Обменные волны при нормальном угле падения не образуются. За- висимость коэффициента отражения обмен- ных волн типа PS от угла падения приведена на рис.1.8.

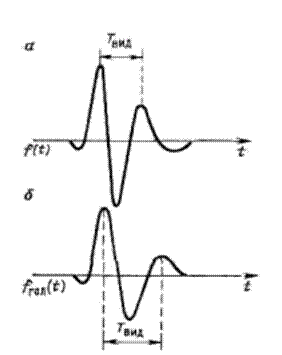
Форма импульса головной волны су- щественно отличается от формы импульса падающей. При больших расстояниях между точкой наблюдений и источником (рис.1.8) импульс смещения головной волны связан с импульсом падающей волны соотношением:

t

f ГОЛ (t ) =òf (t)dt,

(1.18)

(а) и головной (б) волн

где f(τ)—импульс смещения падающей вол- ны. По этой причине спектр головной волны имеет меньшую ширину, больший видимый период и меньшие значения fН , fВ и, fВИД.

Головная волна становится более низкочастотной по сравнению с падающей. Когда расстояние, проходимое волной вдоль преломляющей границы, становится сравнимым с расстоянием R между источником и точкой наблюдения, амплитуда головной волны убывает пропорционально 1/R2.

Дифракция упругих волн. Явление дифракции, известное из оптики, свойственно всем волновым процессам. Оно выражается в том, что возмущение в однородной среде достигает тех точек пространства, которые расположены за препятствием, не пропус- кающим волны. Строгое решение задачи о поле волн в среде с объектом сложной фор- мы возможно только для весьма простых ситуаций. Однако лучевые построения позво- ляют понять причину возникновения дифракции и решить задачу о кинематике этих волн практически во всех интересных для практического использования случаях.

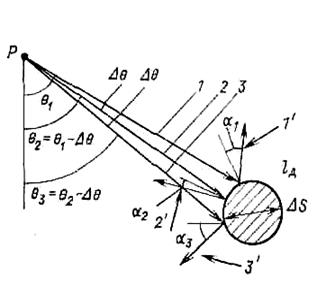
Рассмотрим однородное про- странство, в котором находится неод- нородность с максимальными линей- ными размерами ℓД (рис.1.10). Пусть расстояние от точечного источника до включения значительно превышает ли- нейные размеры его сечения. Если уп- ругие свойства включения отличаются от свойств окружающей среды, то в каждой точке падения волны на этот объект должны образовываться отра- женная и преломленная волны, а лучи их должны идти так, чтобы удовлетво- рять закону Снеллиуса. При малом пе- ремещении точки падения по поверх- ности неоднородности ΔS направление нормали к ней быстро изменяется. Та- ким образом, при малом различии двух

волн на локальной неоднород-

ности.

1—3 — лучи падающей волны;

1`—3` — лучи «отраженных» волн

лучей падающей волны исходящие из точек поверхности ΔS лучи «отражен- ных» и «преломленных» волн будут направлены во все стороны. Включение становится «видимым» во всех точках пространства.

При малом различии θ и θ ± Δθ практически «один» луч падающей волны дает начало лучам, выходящим во всех направлениях. Если размеры включения малы по сравнению с минимальной длиной волны спектра импульса падающей волны, то она достигает всех точек поверхности этого объекта почти одновременно, и эти точки ста- новятся, по принципу Гюйгенса, источниками вторичных волн. Следовательно, к лю- бой точке среды волны, порождаемые фиктивными элементарными источниками, бу- дут приходить также одновременно. Но это означает, что, с точки зрения наблюдателя, включение есть «точка». «Увидеть» отдельные части такого включения окажется не- возможным.

Приведенные рассуждения позволяют на качественном уровне утверждать, что дифракция возникает тогда, когда размер локальной неоднородности сравним с наи- меньшей длиной волны в спектре падающей волны, или поверхность, отделяющая не- однородность от окружающей среды, имеет такие участки, на которых нормаль к ней быстро и в широких пределах изменяет свое направление, когда точка отражения сме- щается на расстояние, сравнимое с наименьшей длиной волны. В обоих случаях в среде

появляются как бы два источника: один истинный и второй, распределенный по дифра- гирующему объему, который возникает только в момент прихода к нему волны от ис- тинного источника. Отсюда становится ясен путь решения кинематических задач ди- фракции: используя принцип Ферма, необходимо найти тот путь от источника до ди- фрагирующего объекта и от этого объекта до точки наблюдения, который обеспечивает минимум времени пробега. Если окружающая среда однородна, то каждый из участков пути есть отрезок прямой линии.

Поверхностные волны. Источник упругих волн обычно располагают на дневной поверхности или несколько ниже ее, в мелкой скважине. Так как плотность воздуха много меньше плотности пород, влиянием воздуха на движение частиц на этой границе (называемой свободной) можно пренебречь. Теоретическое решение, найденное впер- вые Рэлеем, показывает, что на свободной границе развиваются колебания особого ти- па, напоминающие колебания поверхности воды. Эти колебания представляют собой волну с цилиндрическим фронтом. Ось цилиндрического фронта проходит через ис- точник и перпендикулярна к поверхности. Волна, называемая волной Рэлея, распро- страняется радиально вдоль свободной границы. Частицы среды при этом движутся по эллиптическим траекториям в вертикальной плоскости. Однако размах колебаний час- тиц на фронте быстро убывает с удалением от свободной поверхности. На глубинах, сравнимых с v/fвид, волна этого типа практически полностью затухает.

Поверхностные волны могут образоваться и на границах твердого и жидкого по- лупространств (волны Стоунли). По указанной выше специфике распределения энергии их называют поверхностными волнами. Скорость волн Рэлея зависит от коэффициента Пуассона и скорости поперечных волн (она, как правило, не превышает 0,9 vs). При возбуждении упругих волн источниками, расположенными на свободной поверхности, более 60 % энергии источника уходит на образование волн Рэлея, обусловливая их чрезвычайно высокую интенсивность. По мере удаления источника упругих волн от свободной границы интенсивность волн Рэлея резко падает, и, если глубина располо- жения источника превышает v/fвид (где fвид — видимая частота спектра импульса возбу- ждаемых волн), то интенсивность этих волн становится весьма незначительной. Интен- сивность поверхностных волн Стоунли также быстро падает, когда источник припод- нимается над границей твердого и жидкого полупространств так, что расстояние от не- го до дна становится сравнимым с v/fвид.

Отражение от неровных границ. Границы раздела внутри геологической среды во многих случаях заведомо не являются бесконечными плоскостями, для которых по- лучены основные результаты преды-

дущих разделов. Применимость этих результатов к реальным, не плоским и

ограниченным по размерам поверхно-

стям вытекает из строгого решения за-

дачи об отражении сферических волн

от плоской границы. Согласно этому решению, отражение от бесконечной плоской границы формируется не точ-

кой отражения и не всей плоскостью, а

Рис.1.11 К определению локально плоской границы.

1 — вертикальное сечение эллипса, ограничи-

вающего площадь, формирующую отражение

только окрестностью границы вблизи точки отражения, кинематически яв-

ляющейся точкой зеркального отраже-

ния. Для сигнала с узким спектром эта

окрестность практически соответствует первой зоне Френеля преобладающей

гармонической составляющей и имеет форму эллипса, большая ось которого а вытяну- та в плоскости падения, а малая b—нормальна к ней. Величины a и b определяются со- отношениями:

a = 1 ×

l×R1 ×R2

R1 +R2

, b = ×

l×R1 ×R2

(1.19)

где θ — угол падения; R1, R2 — расстояния от точки зеркального отражения до источника и от этой точки до точки наблюдения соответственно; λ0 = v/fвид; v, fвид — скорость и видимая частота спектра падающей волны соответственно. Отсюда следует, что криволинейную границу можно рассматривать как локально плоскую в окрестности каждой точки отражения, если она не более чем на λ0 отличается от плоскости по краям эллипса, ограничивающего площадь, формирующую отражение (рис.1.11). При этом кинематика отраженных волн будет полностью определяться формой отражающей границы и законами Снеллиуса, а динамика—только перепадом акустической жесткости и геометрическим расхождением.

Если на отражающей границе сложной формы имеются локально плоские пло- щадки, такие, что на них образуются точки зеркального отражения относительно точки наблюдения, то они будут порождать боковые волны, аналоги оптических бликов на

поверхности воды. Примером боковых волн является двойное эхо, слышимое в ущелье с крутыми бортами, — отражение от правого и левого бортов. Для границы очень сложной формы в каждой точке наблюдения будет регистрироваться множество отра- женных волн. Граница становится шероховатой, нерегулярной, и применять формулу (1.17) для расчета коэффициента отражения становится невозможно.

Поглощение упругих волн в горных породах. На динамику сейсмических волн в реальных средах большое влияние оказывает степень поглощения сейсмической энер- гии. Поглощение вызывается потерями упругой энергии за счет необратимых процес- сов в среде вследствие ее неидеальной упругости. По этой причине амплитуда, напри- мер, плоской гармонической волны А экспоненциально убывает с расстоянием х, т.е.

А=А0·е-αх (1.20)

где А0 – начальная амплитуда; α – амплитудный коэффициент поглощения.

Амплитудный коэффициент поглощения, различен для разных пород Он возрас- тает с ростом пористости, трещиноватости пород, с уменьшением глубины их залега- ния и водонасыщенности. В среднем у изверженных, метаморфических и сцементиро- ванных осадочных пород α = 10-5 - 10-3 (1/м), у рыхлых осадочных α = 10-3 - 0,5 (1/м). Кроме того, амплитудный коэффициент поглощения зависит от частоты сигнала: он возрастает с увеличением частоты, приблизительно с линейной зависимостью. Поэтому для оценки поглощающих свойств среды часто используют понятие декремент погло- щения

β = α/λ, (1.21)

определяющий ослабление амплитуды гармонического колебания при его распростра-

нении на расстояние, равное длине волны λ.