Основы теории упругости

Теория распространения упругих (сейсмических) волн базируется на теории уп- ругости, так как геологические среды в первом приближении можно считать упругими. Поэтому напомним основные определения и законы теории упругости применительно к однородным изотропным средам.

Установлено, что под действием внешних нагрузок жидкие и газообразные тела изменяют свои объем и форму, деформируются. При деформации частицы тела сме- щаются относительно друг друга и исходного положения. Величина и направление пе- ремещений определяются величиной и характером внешних сил и свойствами тела. Положение частиц тела после деформации можно найти, если известен вектор переме- щений U (х, у, z), отнесенный к исходному положению частиц.

После приложения внешних нагрузок малый параллелепипед, мысленно выделен- ный внутри тела до его деформации, изменит свой объем или форму, или и то, и дру- гое. При этом изменится длина его ребер, а прежде прямые углы между соответствую- щими ребрами станут тупыми или острыми. Количественной мерой деформации явля- ются относительные удлинения ребер малого параллелепипеда и абсолютное измене- ние углов относительно 90°. Таким образом, деформация полностью описывается ше- стью компонентами. Три первые компоненты называются продольными (нормальны- ми) деформациями, три последние — сдвиговыми.

При снятии нагрузки частицы тела могут вернуться или не вернуться в исходное положение. В первом случае говорят об обратимых, а во втором о необратимых дефор- мациях. Тела, в которых развиваются только обратимые деформации, называют упру- гими. Тела, в которых развиваются только необратимые деформации,—пластичными, неупругими. Величина деформаций зависит от величины и характера внешних напря- жений—сил, действующих на единицу площади. Горные породы ведут себя как упру- гие тела только при малых деформациях, когда все шесть компонент деформации не превышают 10-3.

При деформации в упругом теле возникают внутренние напряжения, обусловлен- ные упругим взаимодействием между частицами тела. На каждую площадку малого размера, мысленно выделяемую в теле, действуют напряжения, имеющие в общем слу- чае составляющую, перпендикулярную к площадке,— нормальное напряжение, и две, направленные вдоль площадки, называемые сдвиговыми напряжениями. Три компо- ненты напряжения задаются с помощью шести компонент тензора напряжения. Эти шесть компонент связаны с шестью компонентами малых деформаций законом Гука.

При одноосном сжатии (растяжении) призмы из твердого тела относительное из- менение ее длины вдоль направления действующего напряжения выражается соотно- шением:

W=E D!

!

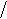(1.1)

где W —величина внешней нагрузки; Е—модуль Юнга; ! — длина призмы; D !

— изменение длины.

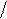Опыт показывает, что удлинение призмы всегда сопровождается сокращением ее

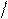поперечных размеров a и b на

Da и

D b . Для изотропных тел

D ! !, Da a, Db b и

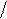
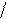
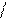(Da a )(Db b)=d

остаются неизменными, независимо от того, каким образом была

ориентирована призма в породе. Модуль Юнга E и коэффициент Пуассона d полно-

стью определяют упругие свойства таких тел. Для анизотропных сред при неизменной осевой нагрузке относительные удлинения ребер призмы будут зависеть от того, как была ориентирована ось призмы в породе, иными словами, упругие свойства зависят от направления внешних нагрузок. Изотропные тела можно описать с помощью упругих констант Ламэ — модуля сжатия l и модуля сдвига m . Эти модули однозначно связа-

ны с модулем Юнга Е и коэффициентом Пуассона d:

E =m(3l+2m)

l + m

(1.2)

d= l

2(l+m)

(1.3)

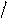При всестороннем сжатии упругих тел, например, путем повышения давления жидкости, в которой расположен образец, объем тел уменьшается. Относительное из- менение объема DV V при этом линейно связано с давлением:

p = kc

×DV V

(1.4)

Коэффициент kc называют модулем всестороннего сжатия. Для изотропных тел связь между kc , λ и μ имеет вид:

k =l+2 m

C 3

(1.5)

В жидкостях и газах μ =0 и kc = λ

Если упругие свойства тел не изменяются при переходе от точки к точке тела, то такие тела называют однородными. В противном случае тело называют неоднородным. В неоднородных изотропных телах λ , μ и kc — функции координат.

При деформации упругого тела под действием внешней нагрузки размеры тела изменяются, например стержень сжимается. Если при снятии внешней нагрузки вся по- тенциальная энергия переходит в кинетическую, то тело называют идеально-упругим. Если же часть энергии уходит на необратимые процессы, например превращается в те- пло, то тело называют вязко-упругим, неидеально-упругим.

Способность тел деформироваться является причиной того, что напряжение от зоны действия внешней нагрузки распространяется на все области тела с конечной ско- ростью, определяемой упругими модулями и плотностью. Распространяющееся в упру- гом теле напряжение порождает деформации — перемещения частиц тела, которые можно измерить. Наблюдения за перемещением частиц тела позволяют эксперимен- тально измерять скорости распространения упругих волн и выявлять различия в физи- ческих свойствах горных пород или их состоянии.