Упругие волны в изотропных средах

Волны и вызывающие их волновые процессы являются особым видом движения, при котором изменение какой-либо величины или состояния среды передается от одной точки среды к другой с конечной скоростью. Отличительной особенностью волновых процессов является то, что событие, происходящее в одной точке среды, через некото- рое время происходит в другой почти в неизменном виде.

Замечательным свойством волновых процессов является то, что, будучи порожде-

ны источником, они начинают существовать автономно, совершенно от него независи-

мо, и протекают и тогда, когда действие источника прекращается. Благодаря этому до нас доходит свет звезды, потухшей миллионы лет тому назад.

Волны в упругих средах возникают всякий раз, когда на какую-либо, часть тела действует изменяющаяся во времени сила. Деформации и напряжения вблизи источни- ка передаются затем всем частям упругого тела за счет упругих связей между частица- ми тела. Передача возмущенного состояния — движения частиц среды — происходит в процессе непрерывного преобразования потенциальной энергии, накапливаемой при деформации, в кинетическую энергию движущихся частиц среды. Этот процесс имеет односторонний характер — энергия забирается от источника и передается упругому телу, в котором она начинает независимое от источника существование, распространя- ясь с конечной скоростью во всем объеме этого тела. Поскольку потенциальная энергия деформированного элемента тела зависит только от величины деформаций и упругих модулей, а кинетическая энергия—от массы элемента и скорости, с которой движется этот элемент, распространение упругих возмущений должно зависеть от упругих моду- лей и плотности тела.

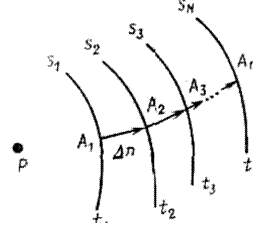
При конечной скорости распространения энергии в каждый момент времени воз- мущение захватывает область конечного размера. Поэтому в любой момент времени существует поверхность, разделяющая возмущенную и невозмущенную области. Эту поверхность называют фронтом возмущения или фронтом волны. Следовательно, распространение возмущения можно описать как разрастание поверхности фронта. Ес- ли в момент t=t1 поверхность фронта задается поверхностью S1, а через очень малый интервал времени Δt в момент t2=t1+Δt — поверхностью S2, то это означает, что воз- мущение с поверхности S1 распространилось на поверхность S2, т. е. прошло в среде некоторый путь. Если в произвольной точке A1(x1, y1, z1) поверхности S1 построить

®

нормаль к этой поверхности

n (A), то она пересечет поверхность S2 в некоторой точке

A2(x2, y2, z2) (рис. 1.1). Отрезок A1A2=Δn —это путь, пройденный волной за время Δt .

®

Направление распространения волны в точке A1(x1, y1, z1) указывается вектором

n(A).

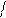Естественно принять, что скорость распространения возмущения (волны) v( A ) =Dn Dt . В общем случае она может зависеть от положения точки A1(x1, y1, z1). Если среда одно- родна, то нет оснований считать, что скорость от точки к точке тела изменяется. В не-

однородной среде, когда изменяются упругие модули и плотность, скорость также мо-

жет стать функцией координат, т. е. v=v(x,y,z).

Рис.1.1 Построение лучевой траектории по известному положению фронтов.

A2A3, и возмущение из точки A1 дойдет до точки A3. При построении нормалей для по-

следующих моментов времени мы найдем точку An, в которую возмущение пришло в момент t=t1+nΔt. Линия A1,A2,…….An дает представление о пути, пройденном волной при распространении из точки A1 в точку An.

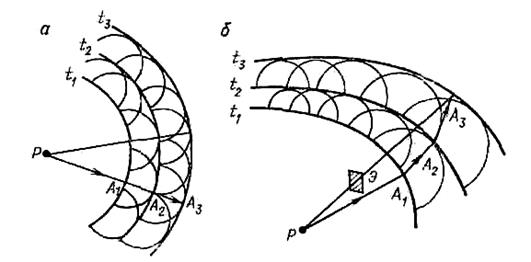
Рис.1.2 Принцип Гюйгенса: образование фиктивных источников в однородной (а) и неоднородной (б) среде.

Траекторию движения возмущения из точки A1 в точку An, а в общем случае — от источника Р к заданной точке — называют лучом. Как следует из рассмотренного по- строения, луч — это линия, всюду нормальная к поверхностям фронтов в точках их пе- ресечения. Таким образом, зная последовательное положение фронтов, можно постро- ить лучи и наоборот.

Построение лучей при известном распределении скорости в среде и заданном по- ложении источника осуществляют на основе принципа Ферма. Для однородных сред и сред с плавно изменяющимися скоростями принцип Ферма утверждает, что возмуще- ние от источника к заданной точке среды распространяется по такому пути, который обеспечивает минимальное время пробега. Для однородных сред минимальное время пробега достигается при минимальной длине пути. Но минимальный путь от источника до точки наблюдения в этом случае— прямая и, следовательно, лучи в однородной сре- де—это прямые линии, выходящие из источника.

Для сред с плавным изменением упругих свойств определение формы лучей тре- бует сложных математических расчетов. Качественно эту задачу можно решить, опира- ясь на принцип Гюйгенса.

Принцип Гюйгенса утверждает следующее: распространение волн любой приро- ды происходит так, как будто при каждом положении фронта на его поверхности ока- зываются точечные источники, генерирующие волны, идущие только вперед. Истин- ный источник как бы переносится в «размазанном» по фронту виде на фронт возмуще- ния. Это означает, что, если положение фронта в момент t1 известно (рис. 1.2), то в со- седний момент времени t2=t1+ Δt положение фронта можно получить путем построе- ния элементарных фронтов от фиктивных источников, возникающих на исходном фронте. Если скорость изменяется плавно, то можно выбрать такой малый интервал времени Δt, что на расстоянии от каждого из элементарных источников примерно Δt·v скорость v можно считать неизменной. Тогда в момент t+Δt возмущение от каждого элементарного источника образует фронт в виде малой сферы с радиусом R=v(A)·Δt. Поверхность, огибающая все элементарные фронты, и является фронтом возмущения в

момент t1+Δt. Теперь фиктивные источники распределены по этой новой поверхности

S2 и можно продолжить построения, определив положение фронта в момент t3= t2+Δt.

Если скорость в среде постоянна, то радиусы элементарных волновых фронтов одинаковы для всех точек, и фронт распространяется как бы параллельным переносом, не искажаясь. Если же среда неоднородна, то в различных точках фронта в момент t1 радиусы R (A) = v(A)·Δt элементарных сферических фронтов будут различными, и но- вая форма будет искажена относительно исходной (рис. 1.2 б). Поскольку лучи всегда должны быть направлены по нормали к фронту в каждой его точке, а фронты не повто- ряют форму друг друга, лучи становятся криволинейными: возмущение из точки A1 по- ступает в точку A3 по пути A1A2A3.

Явление распространения возмущения по криволинейным траекториям называют рефракцией волн. Если на линии «прямой» видимости отрезка PA3 расположен экран Э (непроницаемая для волн перегородка), то этот экран не мешает волнам от источника достигнуть точки наблюдения A3. В однородной среде отрезок PA3 — это луч, по кото- рому волна идет от точки Р к точке A3 и источник Р как бы «не виден». В оптике реф- ракция волн объясняет появление миражей, когда становятся видны объекты, находя- щиеся за горизонтом. В сейсморазведке рефракция обеспечивает выход лучей к земной поверхности и тогда, когда источник возбуждения расположен на той же поверхности или вблизи нее (рис. 1.3), и тем самым создает условия для изучения распределения скорости в толще пород.

Рис.1.3 Выход лучей к земной поверхно-

сти за счет рефракции.

Лучи и фронты дают представление о кинематике волнового процесса—о том, как распространяется возмущение от источника к любой точке в упругом теле. Если в каж- дой точке на луче известна скорость распространения волны v(A), называемая лучевой, то можно найти время, которое волна затрачивает при распространении от источника к любой точке среды, — решить кинематическую задачу. Кинематические задачи подоб- ного типа называют прямыми задачами: по известному распределению скорости в сре- де находят время прихода волны в заданную точку среды.

При решении кинематических задач совершенно несущественно, каков характер возмущения, распространяющегося в изучаемой среде, т. е. как движутся частицы. Ди- намическая теория упругих волн устанавливает, что в однородной изотропной среде возможны волны двух типов. Волны первого типа вызывают такие колебания частиц среды, при которых направление перемещения частиц совпадает с направлением рас- пространения волны. Такие волны называют продольными (Р-волнами). Волны второ- го типа вызывают колебания, при которых частицы смещаются в направлении, перпен- дикулярном к направлению распространения волн. Волны этого типа называют попе- речными (S-волнами). В поперечных волнах вектор перемещения нормален к направ- лению распространения, т. е. к лучу, а луч нормален к поверхности фронта, следова-

тельно, вектор смещения лежит в плоскости фронта. В жидких и газообразных телах распространяются только продольные волны, называемые звуковыми, акустическими.

Продольные и поперечные волны распространяются с различными скоростями (vp

и vs соответственно). Их значения определяют по формулам:

vp =

l+2m

,

s

m

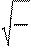vS = s

(1.6)

где σ - плотность.

Поскольку lи mположительны, скорость продольных волн всегда выше скоро-

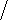сти поперечных. Отношение vP vS

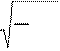l

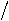vP vS = m+2

(1.7)

- т.е. является параметром, зависящем только от l и m , при этом коэффициент Пуас-

сона:

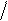( )2 -2

d=vP vS

(1.8)

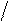
v )2 -2

Поперечные волны бывают двух видов: у одних вектор перемещения имеет толь- ко компоненты, лежащие в вертикальной плоскости, и такие волны называют волнами вертикальной поляризации (SV-волнами); у других—только одну компоненту, лежа- щую в горизонтальной плоскости. Эти волны называют волнами с горизонтальной поляризацией (SH-волнами).

Волновой процесс есть явление, развивающееся в пространстве и времени. На- блюдая за некоторой частицей среды, можно увидеть, что в момент прихода к ней вол- ны частица начинает двигаться, смещаться из положения покоя. Движение ее полно- стью определяется вектором перемещения. Но так как мы рассматриваем только одну

®

частицу, то U следует отнести к x=x1, y=y1, z=z1, характеризующим начальное поло-

жение частицы, после чего ее движение можно изобразить графически. Для этого необ-

ходимо отложить по горизонтальной оси время, а по вертикальной—путь, пройденный

®

в направлении распространения, или любую проекцию

U (x, y, z, t )

на одну из осей

прямоугольной системы координат. Этот график определяет развитие колебаний час-

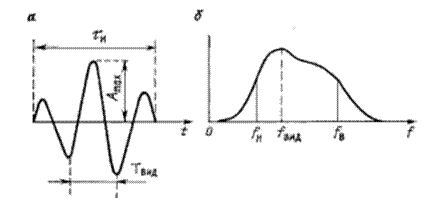
тицы во времени и называется временным импульсом смещения (рис. 1.4 а).

Размах колебаний частицы определяется амплитудой импульса смещения Amax, а продолжительность колебаний—длительностью импульса τи. Каждый источник упру- гих волн характеризуется своей формой импульса U (t).

К моменту окончания импульса смещения в точке (x1, y1, z1) фронт волны уйдет

на расстояние

DR =v(x1, y1,z1)×tи

от этой точки. Следовательно, в один и тот же мо-

мент времени колебания занимают некоторую область среды, ограниченную двумя по-

верхностями, расстояние между которыми

!и =v( x1 ,y1 ,z1 )×tи , где v(x1, y1, z1) — ско-

рость волн в точке (x1, y1, z1). Величину !и называют пространственной длительно-

стью импульса смещения. Пространственная и временная длительности импульса сме-

щения однозначно связаны между собой соотношением

!и =v×tи .

Каждый раз, когда фронт возмущения достигает новой области среды, частицы на фронте начинают движение, повторяющее копирующее движение частиц, через кото-

рые фронт проходил раньше. Импульсы смещения в новых точках, охваченных возму- щением, отличаются друг от друга только размахом, амплитудой. Поэтому говорят, что импульс смещения в волнах, распространяющихся в идеально-упругой среде, не изме- няет свою форму. Эту закономерность можно описать математически:

U(x, y, z, t)=A(x, y, z)·f[t-τ(x, y, z)] (1.9)

где А(x, y, z) — функция, определяющая изменение амплитуды колебаний;

f(t-τ) —функция, определяющая форму импульса смещения;

τ(x, y, z) — время пробега волны от источника до точки с координатами (x, y, z),

причем f(t-τ)=0 при t-τ<0;

t —время, отсчитываемое от момента возбуждения.

Функция А(x, y, z) учитывает изменение амплитуды импульса смещения при уда- лении точки наблюдения от источника — эффект геометрического расхождения. Так как вся энергия, отдаваемая источником в процессе распространения, распределяется по все большей поверхности фронта, энергия, приходящаяся на единицу поверхности фронта, уменьшается, обусловливая и спад амплитуды колебаний частиц среды. Воз- растание поверхности фронта зависит только от формы фронта. Если поверхность фронта—плоскость, то А(x, y, z)=A0=const. Такую волну называют плоской. Источни- ки очень малого размера (в идеале—точечные) создают волну, фронт которой есть сфе- ра с радиусом, возрастающим в однородной изотропной среде по закону R(t)=v·t. Энергия, приходящаяся на единицу поверхности фронта, в этом случае убывает про-

порционально 1/(4πR2), а амплитуда смещений—по закону Am ~1/R. Волну с таким

фронтом называют сферической.

Выявить общие свойства разнообразных импульсов или звуков помогает спек-

Рис.1.4 Временной импульс смещения (а) и его амплитудный спектр (б).

тральный подход. Из курса физики известно, что белый цвет видимого света образуется при наложении простых цветов. Простой цвет соответствует электромагнитным вол- нам, изменяющимся во времени по закону A(t)=A·sin(ωt+φ), где ω=2π/T — круговая частота; f=1/T — частота; T, А — период и амплитуда синусоидальных колебаний со- ответственно. Ощущение цвета изменяется при изменении длины волны λ или частоты, связанных между собой соотношением:

l=с

f

(1.10)

где с — скорость света.

Набор частот определяет частотный спектр видимого света. Амплитуды соответ-

ствующих гармонических составляющих образуют амплитудный спектр.

Аналогичным свойством обладают и сейсмические колебания. Если регистрируют импульс какой-либо волны при наблюдениях в ограниченном интервале времени Tp (например, несколько секунд), то зарегистрированный импульс можно представить в виде суперпозиции гармонических колебаний. Каждое колебание имеет свою ампли- туду, фазу и частоту. Набор амплитуд и фаз называют амплитудным и фазовым спек- тром соответственно. Границы, частотного диапазона при этом задаются верхней и нижней граничными частотами, значения которых зависят только от формы импульса. (см. рис.1.4 б). При спектральном подходе сравнение импульсов различных форм сво- дится к сравнению их частотных диапазонов, задаваемых значениями — верхней и нижней граничными частотами. Импульсы с одинаковыми частотными диапазонами эквивалентны независимо от особенностей их формы.