СИМЕТРІЯ КРИСТАЛІВ ТА ЇХ КЛАСИФІКАЦІЯ

Симетрія кристалів – це закономірне повторення однакових елементів обмеження кристалу (вершин, граней, ребер) відносно уявних ліній, площин, точок (елементів симетрії).

До простих елементів симетрії відносять осі симетрії, площини симетрії, центр симетрії (інверсії).

Центр симетрії С – точка всередині фігури, за відношенням до якої в діаметрально-протилежних напрямках на однакових відстанях знаходяться однакові елементи фігури (рис. 1.1).

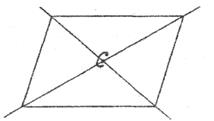
Рис. 1.1. Центр симетрії

Щоб знайти центр симетрії, треба покласти багатогранник на стіл почергово кожною гранню та перевірити чи є зверху грань, що розташована горизонтально; обидві грані (верхня та нижня) – повинні бути однаковими і паралельними. Якщо навіть для однієї з граней не зберігається вказана умова, то центр симетрії відсутній.

Віссю симетрії L_n називається пряма лінія, при обертанні навколо якої на визначений кут 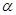фігура суміщається сама з собою. Число суміщень фігури при повторному обертанні (на 360°) визначає порядок осі:

.

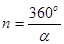В кристалах є осі 1, 2, 3, 4 та 6-го порядку, при цьому а=360,180,120,90,60°. Осі першого порядку не враховуються, тому що в будь-якому кристалі їх необмежена кількість, а осей 5-го порядку та вище 6-го не допускає решітчастість структури кристалів.

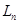
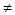
Основний закон симетрії: 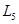і L_>6

Приклади осей різного порядку для плоских фігур показані на рис.1.2.

Рис. 1.2. Осі симетрії плоских фігур

В кристалічних багатогранниках осі симетрії обов'язково проходять через центр ваги фігури, а їх виходи на поверхні співпадають або з вершинами, або з центрами граней, або з серединами ребер (рис.1.3).

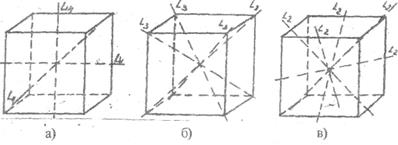
Рис. 1.3. Осі симетрії куба: а) 3L₄, б) 4L₃, в) 6L₂

Для визначення порядку осі симетрії фігуру в точках виходу передбачуваної осі закріплюємо пальцями руки. Запам'ятовуємо вихідне положення всіх елементів обмеження. Обертаючи модель навколо закріпленої осі, спостерігаємо, скільки разів при повному оберті фігура суміститься з первинним положенням: число суміщень, включаючи початкове, є порядком осі. Замітимо, що поки що знайдена єдина вісь, а щоб знайти усі інші, треба таким же чином перевірити попарно усі протилежні вершини, середини граней та ребер.

Для фігур, які не мають центра симетрії, осі симетрії можуть проходити на лініях: вершина – центр грані, центр ребра – центр грані (рис. 1.4).

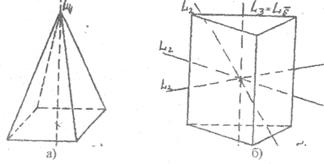
Рис. 1.4 Осі симетрії в несиметричних фігурах

Якщо вісь перпендикулярна до грані, то її порядок відповідає симетрії тієї фігури (рис. 1.2), у вигляді якої надана грань.

Число граней, які сходяться у вершині гранного кута, відповідає порядку осі (рис. 1.3б; 1.4а).

Крім простих осей симетрії існують ще й складні (інверсійні) осі.

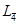
– четверна складна (інверсійна) вісь – завжди співпадає з простою подвійною оссю симетрії (при відсутності центра симетрії). При обертанні фігури навколо цієї осі на 90° та наступному її відображенні в центральній точці фігура суміщається сама з собою.

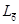– шестерна складна (інверсійна) вісь – завжди співпадає з простою потрійною оссю симетрії (при відсутності центра симетрії) при наявності перпендикулярної до неї площини симетрії ( 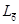= 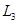+ 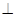P, див. рис. 1.4б).

Площина симетрії Р – площина, що розділяє фігуру на дві дзеркально рівні частини, розташовані відносно одна до одної як предмет та його дзеркальне відображення (рис. 1.5).

Площини симетрії можуть проходити: через середини граней та ребер багатогранника перпендикулярно до них, або через вершини, по ребрах, утворюючи рівні кути з однаковими гранями і ребрами.

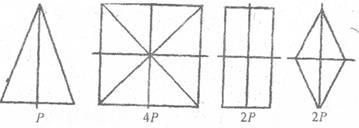
Рис 1.5. Площини симетрії в рівнобедреному трикутнику, квадраті, прямокутнику, ромбі

Максимальна кількість площин – 9 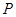у кубі: три взаємно перпендикулярні проходять через середини граней і ребер, шість площин – діагональні (рис.1.6). При визначенні площини симетрії модель необхідно тримати в руках, не перевертаючи її.

Комбінація елементів симетрії для даного багатогранника дає нам кристалографічну формулу симетрії. У формулі на першому місті послідовно записуються осі симетрії (від осей вищого порядку до осей нижчого порядку), а потім площини і накінець центр симетрії. Наприклад, формула симетрії куба 3 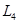∙4L₃∙6L₂∙9PC.

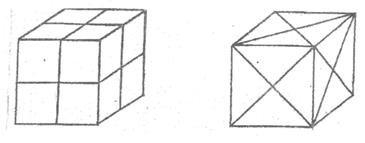
Рис.1.6. Площини симетрії у кубі

Строго математично обгрунтована можливість існування лише 32 комбінацій елементів симетрії, які дають 32 класи симетрії (табл. 1.1). Виведення здійснюється за допомогою теорем взаємодії елементів симетрії.

Теорема 1. Лінії перетину двох площин симетрії є вісь симетрії, кут повороту якої в два рази більший кута між площинами.

Теорема 2. Перетин двох осей симетрії 2-го порядку породжує третю вісь, перпендикулярну до них у точці перетину. Кут повороту цієї осі в два рази більший кута між осями, що перетинаються.

Теорема 3. Взаємодія двох елементів симетрії з трьох: парної осі, перпендикулярної до неї площини і центра симетрії породжує третій, тобто якщо має місце два з них, то обов'язково буде третій.

Теорема 4. Якщо є вісь L_n і перпендикулярно до неї проходить вісь , то число осей буде n.

Теорема 5. Якщо є вісь L_n і паралельно до неї проходить площина симетрії, то число таких площин буде n. Крім того, може бути ще одна перпендикулярна до осі площина симетрії.

Класи симетрії об'єднуються в сингонії (схожо-кутові). Сингонією називається група видів симетрії, які володіють одним або декількома однаковими елементами симетрії при однаковій кількості одиничних напрямків (табл.2).Одиничним напрямком в кристалі називається напрямок, який не повторюється. Наприклад, в тригональній призмі є одна вісь третього порядку 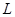₃, в гексагональній – одна вісь шостого порядку .

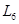В кубі немає одиничних напрямків. Оскільки будь-який напрямок повторюється декілька разів, вони називаються симетрично-рівними.

В кристалі, що має тільки центр симетрії, немає симетрично-рівних напрямків. Усі напрямки тут одиничні.