СИНГОНІЙ

Класифікація кристалів за видом кристалографічних формул ще не дає повної уяви про фігури, що описуються. Так, куб і октаедр належать до однієї й тієї ж кубічної сингонії і характеризуються однією і тією ж формулою (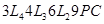), хоча зовнішня їх форма різна. В зв'язку з цим при описуванні кристалів необхідно вміти крім категорії та виду симетрії визначати їх прості форми.

Простою формою називається сукупність граней, які виводяться одна з другою за допомогою елементів симетрії кристалу. Перебравши 32 види симетрії та розглянувши всі можливі випадки розташування граней відносно елементів симетрії, одержимо як результат 47 простих кристалографічних форм (рис. 2.1; 2.2; 2.3).

Назви більшості форм грунтуються на таких древньогрецьких словах:

Моно – один окта – вісім

ді – два додека – дванадцять

три – три едра – грань

тетра – чотири гоніа – кут

пента – п'ять пінаке – дошка

гексa – шість.

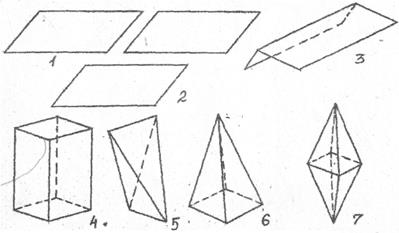
Рис 2.1. Прості форми нижчих сингоній: 1 – моноедр; 2 – пінакоїд; 3 – діедр; 4 – ромбічна призма; 5 – ромбічний тетраедр;, 6 – ромбічна піраміда; 7 – ромбічна діпіраміда

Прості форми підрозділяються на відкриті (не замикаючі повністю простір) – моноедр, діедр, пінакоїд, призми, піраміди та закриті (повністю замикаючі простір) – діпіраміда, ромбоедр, трапецоедри, куб, октаедр, скаленоедри, тетраедри, додекаедри та інш.

Всі прості форми розподіляються за категоріями та сингоніями: для кристалів нижчої категорії можливі 7 простих форм, середньої – 25 , вищої – 15.

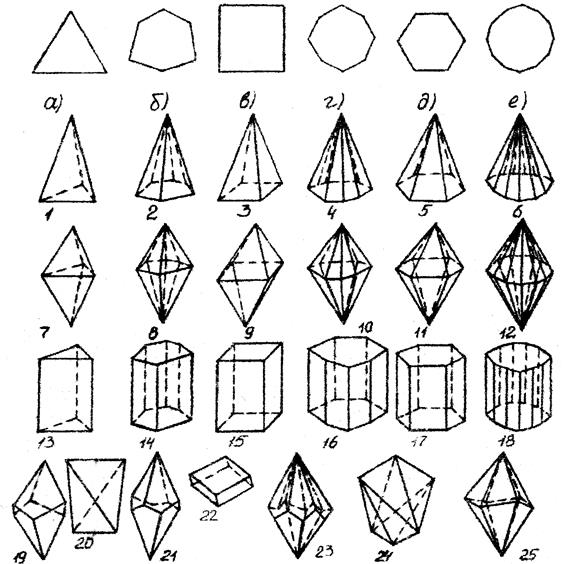
Рис. 2.2. Прості форми середніх сингоній:

піраміди: 1 – тригональна; 2 – дітригональна; 3 – тетрагональна; 4-дітетрагональна;

5 – гексагональна; 6 – дігексагональна;

дипіраміди: 7 – тригональна; 8 – дітригональна; 9 –тетрагональна;

10 – дітетрагональна; 11 – гексагональна; 12 –дігексагональна;

призми: 13 – тригональна; 14 – дітригональна; 15 –тетрагональна;

16 – дітетрагональна; 17 – гексагональна; 18 – дигексагональна;

19 – тригональний трапецоедр; 20 – тетрагональний тетраедр; 21 – тетрагональ-

ний трапецоедр; 22 – ромбоедр; 23 – гексагональний трапецоедр;

24 – тетрагональний скаленоедр; 25 – тригональний скаленоедр;

форми основ і перетинів, перпендикулярних головній осі: а) тригон;

б) дитригон; в) тетрагон; г) дитетрагон; д) гексагон; є) дигексагон

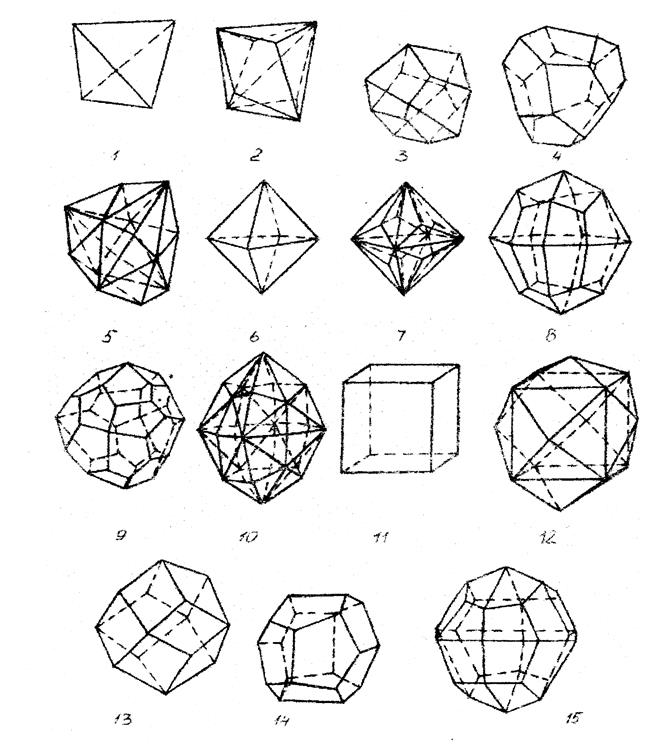
Рис.2.3. Прості форми кубічної сингонії:

1 – тетраедр; 2 – тригон-тритетраедр; 3 – тетрагон-тритетраедр; 4 – пентагон-тритетраедр; 5 – гексатетраедр; 6 – октаедр; 7 – тригон-триоктаедр;

8 – тетрагон-триоктаедр; 9 – пентагон-триоктаедр; 10 – гексаоктаедр;

11 – гексаедр; 12 – тетрагексаедр; 13 – ромбододекаедр;

14 – пентагон додекаедр; 15 – дидодекаедр

Сукупність декількох простих форм, об'єднаних в єдиний багатогранник через елементи симетрії, називається комбінованою формою.

В реальних кристалах грані однієї простої форми відсікають грані іншої простої форми, і в такому (усіченому) вигляді розшифрування комбінацій форм утруднене.

Рекомендуємо користуватися такими положеннями:

1. Передусім, визначивши кристалографічну формулу багатогранника, встановити сингонію та категорію.

2. Підрахувати кількість сортів граней. Сорт - це грані однакових форм і розміру.