Физические процессы, протекающие при амплитудной модуляции
 Наиболее простым методом получения амплитудно-модулированных колебаний является метод, который ранее использовался в маломощных телефонных передатчиках (рис. 4.1.3):
Наиболее простым методом получения амплитудно-модулированных колебаний является метод, который ранее использовался в маломощных телефонных передатчиках (рис. 4.1.3):
|
Звуковые колебания, воздействующие на угольный микрофон, вызывают колебания его мембраны, которая изменяет сопротивление угольного порошка.
Звуковое давление Р, воздействующее на микрофон, является произвольной функцией времени Р = f (t). Для упрощения рассмотрения процессов, протекающих при амплитудной модуляции, сделаем следующие допущения:
а) звуковое давление, воздействующее на микрофон, изменяется по синусоидальному закону:
P = Pm · sin Ω t,
b) проводимость микрофона Ym является линейной функцией звукового давления:
Ym = a · P;
Проводимость антенной цепи определяется следующим выражением:
YА = Y0 + Ym ;
где Y0 – начальная проводимость антенной цепи (при P = 0).
Тогда YА = Y0 · ( 1 + 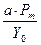 · sin Ω t );
· sin Ω t );
Напряжение высокочастотных синусоидальных колебаний несущей частоты ω0, вырабатываемых генератором, равно:
U = Um · sin ω0 t;
Ток в антенне равен: IA = U · YА;
IA = U m · Y0 · (1 + 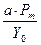 · sin Ω t ) · sin ω0 t;
· sin Ω t ) · sin ω0 t;
Ток в антенне при отсутствии модуляции равен:
I 0 = U m · Y0 ;
Тогда IA = I 0 · (1 + 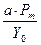 · sin Ω t) · sin ω0 t ;
· sin Ω t) · sin ω0 t ;
Таким образом, процесс модуляции заключается в перемножении двух функций времени:
1 + 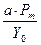 · sin Ω t и I 0 · sin ω0 t ;
· sin Ω t и I 0 · sin ω0 t ;
Результат этого перемножения может быть представлен следующим образом:
IA = I 0 · sin ω0 t + I 0 · 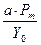 · sin Ω t ·sin ω0 t ;
· sin Ω t ·sin ω0 t ;
После преобразования получаем:
IA = I 0 · sin ω0 t + 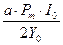 · [cos (ω0 – Ω) t – cos (ω0 + Ω) t];
· [cos (ω0 – Ω) t – cos (ω0 + Ω) t];
Здесь первый член является колебанием несущей частоты ω0, а второй – включает частоты, отличающиеся от несущей частоты на величину, равную частоте модуляции Ω. Эти частоты называются боковыми частотами.
Частотный спектр амплитудно-модулированных колебаний при модуляции тональным сигналом приведен на рис. 1.1.4.

Рис. 4.1.4. Частотный спектр амплитудно-модулированных
колебаний при модуляции тональным сигналом с частотой Ω
Если модулирующее напряжение не является синусоидальным сигналом, а описывается произвольной функцией F(t), то в этом случае получаются две боковые полосы частот модулированного сигнала (рис. 4.1.5).
 | |||
| |||
Следовательно, при амплитудной модуляции частотный спектр модулированного сигнала состоит из несущей частоты и двух боковых полос, ширина каждой из которых равна ширине спектра модулирующего сигнала. Таким образом, спектр амплитудно-модулированного колебания вдвое шире, чем спектр модулирующего сигнала.
В результате приведенного анализа выражения для тока, протекающего в антенне, можно сделать следующие выводы:
1. При передаче амплитудно-модулированных колебаний электромагнитная энергия излучается:
– на несущей частоте;
– в нижней боковой полосе частот;
– в верхней боковой полосе частот.
2. Значения тока несущей частоты является функцией времени и не зависит от амплитуды модулирующих низкочастотных колебаний. Это означает, что несущая частота не содержит информации о модулирующем сигнале.
3. Значения токов боковых полос является не только функцией времени, но и функцией звукового давления, воздействующего на микрофон. Таким образом, вся информация о модулирующем сигнале передается в нижней и верхней боковых полосах.
4. Значения токов обоих боковых полос определяются одним и тем же коэффициентом, содержащим величину звукового давления. Это означает, что в нижней и верхней боковых полосах передается совершенно одинаковая информация, т. е. происходит дублирование передаваемой информации.
Дата добавления: 2015-06-22; просмотров: 763;
