Решение математических задач с помощью НЛ-10м

Небольшие графические схемы, подсказывающие как решить ту или иную задачу на линейке, в авиации издавна называют «ключами». Ключ показывает, на каких шкалах следует устанавливать исходные данные, как шкалы должны быть сдвинуты друг относительно друга и где отсчитать ответ. Здесь приведены только несколько самых распространенных ключей. Другие будут рассмотрены в последующих главах, а некоторые уже использовались в главах предшествующих..

1) Умножение чисел. Умножение можно выполнить на шкалах 1 и 2 в соответствии с ключом, изображенным на рис.4.2

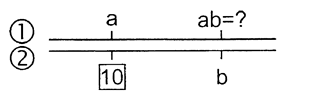
Рис. 4.2. Умножение чисел

В соответствии с этим ключом число 10 на шкале 2 линейки (оно обведено квадратом, чтобы легче найти) следует, сдвинув движок, установить на множимое а по шкале 1. Тогда напротив множителя b (на шкале 2) можно по шкале 1 отсчитать произведение аb..

2) Деление чисел. Деление - операция обратная умножению Ключ для ее выполнения изображен на рис. 4.3.

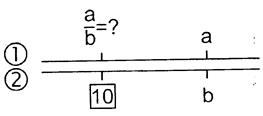Рис. 4.3. Деление чисел

По ключу на шкале 1линейки откладываем делимое а, напротив, на шкале 2, устанавливаем делитель b, по шкале1 напротив прямоугольного индекса с цифрой 10 получаем частное.

3) Умножение и деление числа на тригонометрическую функцию.

Для умножения любого числа а на синус или тангенс какого-либо угла а необходимо установить черный треугольник, нанесенный на шкале 4, на число а по шкале 5 и напротив значения угла а отсчитать на той же шкале 5 результат умножения, то есть a tgα (a sinα, acosα). При умножении на сину угол следует установить на шкале синусов, а при умножении на тангенс - - на шкале тангенсов (рис. 4.4)..

а 90°-а

Рис. 4.4. Умножение на тригонометрическую функцию

Умножение числа на косинус угла также выполняется с помощью шкалы синусов. При этом используется известный факт, что косинус угла а равен синусу (90°- а). Следовательно, для умножения на косинус на шкале 3 нужно установить не сам угол, а его дополнение до 90° .

4) Деление числа на тригонометрическую функцию. Деление - операция обратная умножению. Найти частное от деления числа, например, на синус угла - это значит найти такое число, которое при умножении на синус даст исходное число.

Чтобы разделить число на тригонометрическую функцию необходимо совместить число на шкале 5 и значение угла (на шкале синусов или тангенсов, в зависимости от вида тригонометрической функции). Результат можно отсчитать напротив черного треугольника. На рис.4.5 показан ключ на примере деления на тангенс.

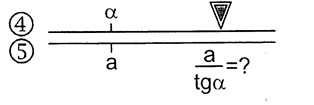Рис. 4.5. Деление на тангенс

При делении на косинус на шкале устанавливается не сам угол, а его дополнение до 90°.