Http://nanophysics.ac.ru/mezo.htm

Один из основных разделов квантовой нанофизики - физика мезоскопических систем. Слово "мезоскопика" (в применении к физике) было заимствовано В.ван Кемпеном и М.Азбелем из палеонтологии и в применении к физике используется для обозначения сравнительно малых систем, число частиц в которых слишком велико для того, чтобы применять уравнения механики (в данном случае, квантовой), но слишком мало для использования статистики: флуктуации величин, характеризующих систему в целом, оказываются порядка их средних значений. В металлах характерным масштабом длины, разделяющим мезоскопические и макроскопические системы, является длина L_phi, на которой сохраняется фаза волновой функции электрона. В процессах, происходящих на размерах L < L_phi, необходимо учитывать интерференционные эффекты от электроных волн, прошедших по различным возможным путям. Длина фазовой когерентности L_phi выделяет "мезообласти", интерференция внутри которых определяет поведение всего макрообъекта. Впервые понятие длины фазовой когерентности L_phi было введено в 1979 г. в работе Л.Горькова, А.Ларкина и Д.Хмельницкого из ИТФ им. Ландау, посвященной вычислению температурной зависимости проводимости тонких металлических пленок при очень низких температурах. Эта работа впоследствии оказалась одним из тех нескольких "камней", которые образовали фундамент квантовой нанофизики.
Экспериментальное изучение мезоскопических явлениий началось с опытов Ю.В.Шарвина и Д.Ю.Шарвина, выполненных в Институте физических проблем РАН им.П.Л.Капицы в 1981 году. Изучая тонкие пленки нормальных металлов, напыленных на тонкие кварцевые нити, они обнаружили осцилляции сопротивления в продольном магнитном поле, и показали, что эти осцилляции обусловлены интерференцией электронов, сохраняющих фазовую когерентность при упругих столкновениях при низких температурах. Эти экспериментальные результаты послужили мощным импульсом к началу экспериментальных исследований разнообразных электронных явлений в мезоскопических системах.
Важным направлением в мезоскопике является изучение флуктауций тока и напряжения, поскольку из-за относительно небольшого числа каналов проводимости флуктуационные части этих величин могут оказаться вовсе не малы по сравнению с их средними значениями. Теория дробового шума в мезоскопических проводниках начала свое развитие около 10 лет назад, главным образом начиная с работ Г. Лесовика (ИТФ им. Ландау). В настоящее время активно развиваются и экспериментальные исследования по этому направлению.
Одним из очень важных порождений мезоскопики, перспективных с точки зрения приложений, является одноэлектроника (иначе говоря, группа явлений, в которых существенна кулоновская блокада проводимости). Когда размер частиц металла или полупроводника d мал, мала и их емкость C ~ d; тогда перенос одного электрона с одной частицы на другую приводит к изменению энергии порядка E_C = e²/2C. При достаточно низких температурах T <= E_C перенос электронов может быть существенно затруднен, что и называется кулоновской блокадой проводимости. Величиной зарядовой энергии можно управлять, изменяя напряжение на дополнительном электроде. Такие приборы с варьируемой кулоновской блокадой называют одноэлектронными транзисторами. Первые теоретические разработки в этой области были сделаны К.Лихаревым и Д.Авериным (Физфак МГУ) в середине 80-х годов.

4) С длиной фазовой когерентности

Длина фазовой когерентности определяется как расстояние, на котором сохраняется постоянной фаза бегущей электронной волны. Такое расстояние должно быть соизмеримо с длиной свободного пробега электрона. После неупругого рассеяния электронной волны возникает некогерентность вторичных электронных волн, что приводит к сдвигу фаз между вторичными волнами. Постоянство фазы электронных волн позволяет модулировать разницу фаз между электронами и управлять проводимостью наносистем на уровне отдельных квантов, используя явление интерференции.

5) С длиной волны электрона (волна Де-Бройля)

В случае, если размеры нанобъекта сопоставимы с длиной волны электрона могут возникнуть следующие квантовые наноструктуры:

· квантовые ямы, когда в одном из трех направлений (рис.) размеры соизмеримы с длиной волны, а в остальных значительно больше длины волны,

· квантовые проволоки (волокна), когда в двух из трех направлений (рис.) размеры соизмеримы с длиной волны, а в третьем значительно больше длины волны,

· квантовые точки, когда во всех трех направлениях (рис.) размеры соизмеримы с длиной волны.

Электрон, оказавшись, например, в квантовой яме может относительно свободно перемещаться в направлениях, где длина его волны будет существенно меньше размера нанообъекта (рис. 2). В третьем направлении он окажется ограниченным в перемещении за счет появления стоячей волны, то есть будет находиться в стационарном энергетическом состоянии, подобно электрону в атоме.

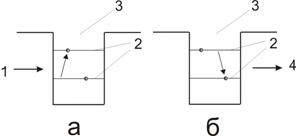
Рис.2. Переходы межу энергетическими уровнями в квантовой яме а) в фотоприемнике (1 – излучение, стимулирующее переход между уровнями 2 в квантовой яме 3, б) в источнике излучения 4 – излучение из источника, вызванное переходом между уровнями 2 в квантовой яме 3.

6) С длиной спиновой релаксации

Электрон при своем движении в упорядоченном магнетике, например, ферромагнетике, на некотором расстоянии (1 – 10 нм) сохраняет направление спина. Это позволяет наблюдать эффекты спинполяризованного транспорта, в частности, гигантское мгнитосопротивление в нанообъектах, имеющих соответствующие размеры, равные длине устойчивости спина электрона.

В материалах, обладающих магнитным порядком (ферро, ферри, антиферромагнтиках) присутствует вклад в электросопротивление, вызванный рассеянием электронов проводимости на магнитных моментах атомов (магнетосопротивление). В значительной степени сопротивление возрастает в тонких наноразмерных слоях магнетиков при прохождении электрона через слои с разным направлением упорядоченных магнитных моментов (гигантское магнетосопротивлении). Возможности использования таких нанослоев реализованы в магнитном (спиновом) вентиле (рис.1).

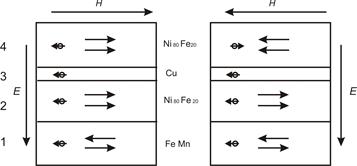
Рис. 1. Спиновый вентиль.

В первом антиферромагнитном слое (FeNi) направление магнитных моментов постоянно. Во втором ферромагнитном слое (Ni₈₀Fe₂₀) направление магнитных моментов также постоянно и определяется первым слоем. Выше третьего, диамагнитного слоя (Cu), расположен еще один ферромагнитный слой (Ni₈₀Fe₂₀), направление намагничивания которого легко изменяется под действием управляющего магнитного поля H. При прохождении электрона под действием электрического поля E через нанслои вентиля снизу вверх его движение возмущается в наименьшей степени, если слои ферромагнитных слоев параллельны (рис.1 слева). В случае антипараллельности ферромагнитных слоев (рис.1 справа) электрон вынужден поменять направление спина, что увеличивает сопротивление его движению и способствует росту электрического сопротивления вентиля.

Квантовый эффект Холла

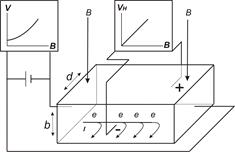
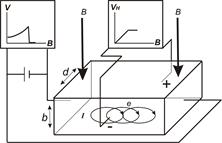
Пусть перпендикулярно верхней и нижней грани полупроводниковой пластины толщиной b и шириной d (рис.1) проходят силовые линии магнитного поля B. Если к торцевым граням пластины приложить напряжение, то вдоль пластины перпендикулярно линиям поля будут двигаться заряды, испытывая действие силы Лоренца, искривляющей траекторию их движения. При этом заряды будут смещаться к одной и боковых граней пластины, создавая разность потенциалов, называемую ЭДС Холла V_H.

а) б)

Рис.1 . Эффект Холла в классическом (а) и квантовом варианте (б).

Исходя из равенства сил, действующих на заряд в направлении его смещения можно записать

E e = e v B = V_H e/d

Используя выражение для силы тока

I = n e v b d

получим

V_H = I B/(e n b)

Отсюда сопротивление Холла

R_H = V_H/ I = B/(e n b),

изменяется пропорционально индукции B (рис. 1)

Было обнаружено, что при уменьшении толщины пластины до наноразмеров (одномерный нанообъект) и при очень низких температурах (~ 1К) R_H и больших значениях магнитной индукции (~ 30Тл)на кривой R_H(H) возникают ступени (рис.), соответствующие неизменности сопротивления при изменении магнитного поля. Возникновение этих ступеней объясняется тем, что электроны в присутствии магнитного поля подвергаются дополнительному квантованию, то есть располагаются на определенных энергетических уровнях (уровнях Ландау). Энергия электронов при этом принимает дискретные значения ~h/ie², где i – целое число, а h/e² = 25,813807449 КОм является квантом сопротивления, используемым в качестве эталона сопротивления R_К-90, независящим от материала проводника и геометрии образца.

Обычное сопротивление вдоль направления тока в присутствии магнитного поля, называемое магнетосопротивлением

R = V/ I = B V/ (V_H e n b)

При постоянстве R_H обращается в ноль V и магнетосопротивление R.