Соизмеримость размеров нанообъектов с характерными длинами, связанными с физическими параметрами.

1) С длиной свободного пробега электрона:

Как известно, поведение электронов при их движении на расстояниях более 10 нм может быть описано, например, в случае кремния, без учета влияния размеров элементов электронной схемы. При меньших предельных расстояниях перемещения электрона необходим учет эффектов, связанных с изменением размеров элементов. Это вызвано проявлением корпускулярно-волнового дуализма частиц, описанного уравнением де Бройля:

h = m u l,

где h – постоянная Планка, m- масса частицы, u – скорость частицы, l - длина волны.

Так, в кремнии l составит несколько меньше 10 нм, что способствует проявлению в соответствующих наноразмерных объектах характерных волновых явлений – интерференции и дифракции. Для материалов с меньшей эффективной массой (в частности, 0,067 m₀ для электронов в арсениде галлия) этот предел наступает и при больших размерах. Результатом интерференции и дифракции может быть осцилляция электропроводности, связанная с появлением стационарных энергетических состояний электронов. Например, в тонких пленках тантала и висмута нанометровой толщины обнаружена осциллирующая зависимость проводимости с периодом 5 нм для Та и 23 нм для Bi. Такое поведение определяется квантовым размерным эффектом в пленках металла, приводящим к квантовым осцилляциям проводимости.

Поэтому для уменьшения размеров нанобъектов, используемых в полупроводниковой технике по традиционной технологии, существует ограничение. Дальнейшее усовершенствование основано на принципах, использующих проявление квантовых закономерностей (спинтроника, туннелирование и т.п.)

2) С диффузионной длиной:

Существует диффузионное движение носителей, обусловленное:

- хаотическим тепловым движением (самодиффузия),

- направленным движением под действием градиента концентрации,

- диффузией носителей, вблизи дефектов.

Под действием градиента концентрации зарядов в полупроводниках возникают диффузионные токи, прекращающиеся после выравнивания концентрации. Диффузионный ток I носителей заряда q описывается выражением

I = qDdn/dx,

где D – коэффициент диффузии, dn/dx – градиент концентрации.

Коэффициент диффузии D подчиняетсясоотношению

D = mkT/q,

где m = (ql)/(mu) подвижность носителей заряда.

В наноразмерных полупроводниковых объектах, где размер нанообъекта соизмерим с длиной свободного пробега l, обеспечивается максимально возможный диффузионный ток в пределах нанообъекта.

3) С длиной экранирования:

В несобственных полупроводниках всегда присутствуют ионизированные примеси, создающие центры рассеяния свободных носителей заряда. Свободные носители экранируются от ионизированных примесей теми же свободными носителями, но более близко расположенными к стационарным ионам. Это вызывает экранировку от стационарных ионов части свободных носителей.

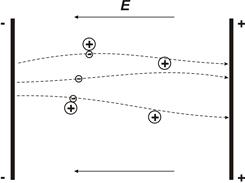
Рис. 1. Частичная экранировка среднего электрона боковыми электронами от положительных примесных ионов

Экранировка

Потенциал ионизированных примесей с учетом экранирования уменьшается с расстоянием r пропорционально exp-(r/l_s), где l_s – длина экранирования – расстояние, при котором потенциал ионизированных примесей ослабевает в e раз.

l_s =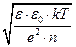

где e - относительная диэлектрическая проницаемость среды, n - концентрация носителей заряда. Длина экранирования называется также Дебаевским радиусом.

В несобственных полупроводниках l_s ~ 10 – 100 нм, что соответствует размерам нанообъектов.

Чем меньше длина l_s тем меньше искажена траектория движения электронов в нанообъектах, что укорачивает их путь и уменьшает время перемещения, например, между истоком и стоком в МОП-транзисторах. Это способствует увеличению быстродействия электронных схем.

Управление длиной экранирования находит также использование в попытках реализации быстрого ионного транспорта в суперионных проводниках за счет формирования структурно-упорядоченных гетеропереходов, позволяющих создать конденсаторы с удельной емкостью 0,1 мкФ/см² и рабочей частотой 1 ГГц. Их возможное применение: емкостная энергозависимая память объемом более 5 Гбит, источники питания для наносистем.

Характеристикой суперионных проводников является параметр

P = l_s/d,

где d – толщина разупорядоченного слоя гетероперехода.

Чем больше длина экранирования и меньше d, тем лучшей проводимостью обладает суперионный проводник.

При удельной емкости ~ 10^-4 Ф/см² на упорядоченном гетеропереходе накапливается заряд ~ 10^-4 Кл/см, что соответствует плотности зарядов на поверхности ионных кристаллов. Это явление гигантского накопления электрического заряда на гетеропереходах открыто в Институте проблем технологии микроэлектроники в 2005 г. Наноэффект в данном случае является следствием использования технологии атомной точности.