Принцип аргумента

Пусть дано характеристическое уравнение:

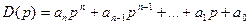
Это уравнение можно записать через его корни:

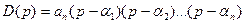
где a₁, a₂, …,a_n - корни полинома D(p).

Выполним подстановку 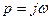и перейдем в частотную область:

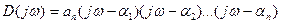
Представим элементарный множитель ( 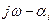) в виде вектора на комплексной плоскости и рассмотрим его поведение при изменении w от -¥ до +¥.

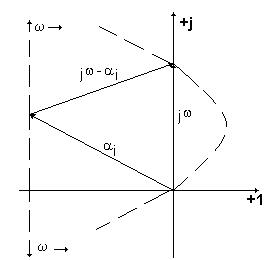
Суммарный угол поворота равен 180⁰.

Для корня с отрицательной вещественной частью вектор ( 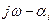) поворачивается против часовой стрелки на 180⁰. Обозначим этот разворот как приращение аргумента элементарного вектора:

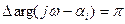для изменения частоты w от -¥ до +¥.

Для корня с положительной вещественной частью приращение аргумента составит

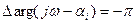
Если система устойчива, то все корни имеют отрицательную вещественную часть и приращение аргумента для всей функции D(jw):

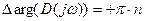
Если рассмотреть только действительные значения частоты от 0 до +¥, то

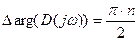
Критерий устойчивости Михайлова

Используя принцип аргумента, исследуем поведение функции 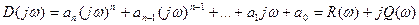при изменении w от 0 до +¥.

Для любого значения частоты w имеем вектор , который будет поворачиваться при изменении частоты. Траектория конца вектора называется годографом Михайлова. Принцип аргумента позволяет сформулировать критерий устойчивости Михайлова:

САУ будет устойчива, если годограф функции 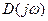начинается на положительной вещественной полуоси 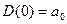и проходит последовательно n квадрантов (где n – порядок характеристического уравнения) нигде не обращаясь в нуль, и нигде не нарушается порядок следования квадрантов.

Пример устойчивых:

Пример неустойчивых:

Если годограф проходит через начало координат, то система находится на границе устойчивости.

Условие нахождения на границе устойчивости: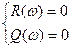

Формулировка может звучать иначе:

Для устойчивой САУ годограф начинается на вещественной положительной полуоси и должен поочередно пересекать мнимую и вещественную ось.

Для устойчивой САУ вещественные и мнимые части годографа Михайлова должны по очереди пересекать ось абсцисс.