Проверка гипотез
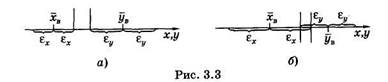
В медико-биологических исследованиях актуальной является задача сравнения выборок, полученных в результате эксперимента, заключающегося в том или ином воздействии на объект. Фактически конечный результат исследования зависит от достоверности различий значений случайной величины в контроле (до воздействия или без него) и опыте (после воздействия). Наиболее просто решается задача определения достоверности различий статистических распределений, если предварительно для выборок рассчитаны доверительные интервалы. Положим, есть два статистических распределения некоторых случайных величин X и У. Пусть генеральные средние этих распределений с доверительной вероятностью р = 0,95 находятся в доверительных интервалах (хв ± ех) и (ув ± s ), и пусть при этом ув > хв. Если соблюдается неравенство (г/в - ε ) > (хв + ε), то не вызывает сомнения, что случайная величина У существенно больше случайной величины X (см. рис. 3.3, а). Вероятность этого превышает 0,95.
На рис. 3.3, б представлен вариант, когда выборки частично пересекаются, т. е. когда выполняется неравенство (ув - еу) < (хв + гх). В этом случае целесообразно оценивать достоверность различий выборочных средних хв и ув с помощью дополнительных расчетов. Наиболее просто это сделать, предполагая, что случайные величины X и У распределены по нормальному закону. Условием существенности различия двух опытных распределений, являющихся выборками из различных генеральных совокупностей, является выполнение следующего неравенства для опытного и теоретического значений критерия Стьюдента: toa > teop. Для нахождения значения tов используют следующую формулу:

Здесь σх и σy — выборочные средние квадратические отклонения, пх и пу — число вариант в выборках (объемы выборок), хв и yв — выборочные средние значения.
Теоретическое значение tTeop находят по таблице 10, входными величинами которой являются доверительная вероятность р и параметр , связанный с числом вариант в выборках. Этот параметр определяют следующим образом. Если ах ≈σ , то f = пх + п - 2. Если же ах и а различаются на порядок и более, то величина определяется по формуле:
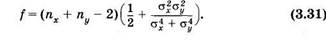
Используя этот способ оценки достоверности различия выборочных средних значений двух выборок, следует придерживаться такой последовательности действий. Во-первых, по экспериментальным данным нужно найти значения выборочных средних и средних квадратических отклонений для каждой выборки. Затем, сравнив величины σх и σy, найти величину f. После этого следует задать определенное значение доверительной вероятности и по таблице 10 найти tтеор. Затем по формуле (3.30) рассчитать ion.
Если при сравнении теоретического и опытного критериев Стьюдента окажется, что tou > tTeop, то различие между выборочными средними значениями случайных величин X и Y можно считать существенным с заданной доверительной вероятностью. В противоположном случае различия несущественны.
Представленный выше способ оценки достоверности различий выборок по выборочным средним является довольно простым. Существует большое число тестов и критериев для сравнения выборок и составления заключения о достоверности их различий. Как правило, при этом рассматривают вероятность двух взаимоисключающих гипотез. Одна из них, условно называемая «нулевой» гипотезой, заключается в том, что наблюдаемые различия между выборками случайны (т. е. фактически различий нет). Альтернативная гипотеза означает, что наблюдаемые различия статистически достоверны. При этом для оценки обоснованности вывода о достоверности различий используют три основных доверительных уровня, при которых принимается или отвергается нулевая гипотеза. Первый уровень соответствует уровню значимости (30 < 0,05) для второго уровня ро < 0,01. Наконец, третий доверительный уровень имеет р0 < 0,001. При соблюдении соответствующего условия нулевая гипотеза считается отвергнутой. Чем выше доверительный уровень, тем более обоснованным он считается. Фактически значимость вывода соответствует вероятности р = 1 . В медицинских и биологических исследованиях считают достаточным уже первый уровень, хотя наиболее ответственные выводы предпочтительнее делать с большей точностью. Одной из методик, позволяющих судить о достоверности различий статистических распределений, является ранговый тест Уилкоксона. Под рангом (Ri) понимают номер, под которым стоят исходные данные в ранжированном ряду. Если в двух сравниваемых выборках данному номеру соответствуют одинаковые варианты, то рангом этих вариант является среднее арифметическое двух рангов — данного и следующего за ним (см. пример). Покажем, как используется этот тест на примере сравнения двух равных по объему выборок.
Измеряли массу 13 недоношенных новорожденных (в граммах) в двух районах А и Б большого промышленного центра, один из которых (Б) отличался крайне неблагоприятной экологической обстановкой. Получены два статистических распределения (А) и (Б):
А: 970 990 1080 1090 1110 1120 ИЗО 1170 1180 1180 1210 1230 1270
Б: 780 870 900 900 990 1000 1000 1020 1030 1050 1070 1070 1100
Следует решить вопрос о том, достоверны ли различия между этими статистическими распределениями.
Составим общий ранжированный ряд с указанием номеров соответствующих вариант (RA Б) — рангов (строки А и Б соответствуют выборкам):

Как видно, варианта 990 встречается в первой и второй выборках, поэтому для нее рангом является среднее арифметическое значение 6 и 7.
Далее в ряду остаются лишь варианты первой выборки, поэтому ряд не закончен. Нулевая гипотеза состоит в том, что различий между выборками нет (они случайны и потому несущественны). Ранговый тест учитывает общее размещение вариант и размеры выборок, но не требует знания типа распределения. Основной вывод о верности нулевой гипотезы делается на основании анализа минимальной суммы рангов (из двух сумм для сравниваемых выборок), т. е. критерием является величина Т = ЯБ (учитывая, что Rв < Z -RA). При этом пользуются специальными таблицами. В частности, если число вариант в выборках одинаково (п1 = п2).
Критические значения величины r (теста Уилкоксона) при п1 = п2 = п для разных значений уровня значимости/
В этой таблице указаны две входные величины: число вариант в выборках и значение третьего и второго уровней значимости (Ро = 0,05 и 0,01). В нашем случае Т = RB = 110,5, что меньше табличного значения для п = 13 и βо < 0,01. Следовательно, на втором уровне значимости (р > 0,99) можно отвергнуть нулевую гипотезу. Таким образом, различия выборок достоверны с вероятностью, превышающей 0,99.
Дата добавления: 2015-06-22; просмотров: 744;
