КИНЕМАТИКА 4 страница

Решение. Опять рассмотрим механическую систему, состоящую из плиты и груза D), и изобразим действующие на нее внешние силы 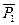, 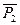и реакцию 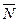(рис. Д2а). Для определения N₁ воспользуемся теоремой о движении центра масс системы и составим дифференциальное уравнение его движения в проекции на ось у:

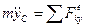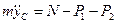или , (9)

где m — масса системы; Р₁ = m₁g; Р₂ = m₂g. Из формулы, определяющей ординату 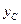центра масс системы, следует, что для рассматриваемой системы 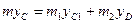где, как видно из рис. Д2а, 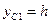, 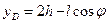. Тогда, используя равенство (7), получим

.

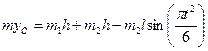Вычисляя производные и учитывая, что h = const, получим

,

.

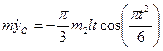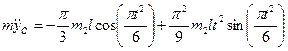Подставив это значение 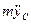в равенство (9), найдем зависимость N от t и из нее, полагая t = t₁ = 2 с, определим искомую величину N₁.

Ответ: N₁ =197,3 Н.

4. Определение угловой скорости ω. Плита вращается вокруг оси z, лежащей в плоскости плиты (рис. Д2в), и в момент времени t₀ =0, когда угловая скорость плиты равна ω₀, на нее начинает действовать вращающий момент М.

Дано: дополнительно к условиям (1): ω₀ = 5 c^-1 , M = kt, где k = 10 Н*м/с.

0пределить: ω = f(t) — зависимость угловой скорости плиты от времени.

Решение. Рассмотрим механическую систему, состоящую из плиты и груза D, и изобразим действующие на нее внешние силы: силы тяжести 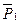, 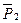и реакци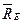и и 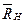подпятника и подшипника и вращающий момент М.

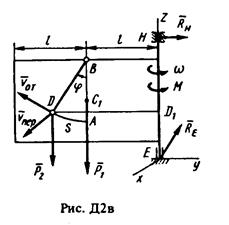
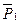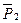Для определения ω применим теорему об изменении кинетического момента системы относительно оси z. Предварительно заметим, что так как силы и , параллельны оси z, а реакци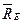и и 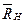эту ось пересекают, то их моменты относительно оси z равны нулю. Тогда 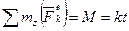и теорема дает

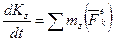или 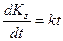. (10)

Умножая обе части этого уравнения на dt и интегрируя, получим

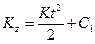. (11)

Для рассматриваемой механической системы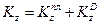

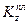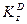где и — кинетические моменты относительно оси z плиты и груза О соответственно. Поскольку плита вращается вокруг оси z, то

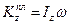, где 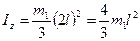. (13)

Для определения 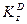рассмотрим движение груза как сложное, считая его движение по отношению к плите относительным, а вращение плиты вокруг оси z — переносным движением. Тогда 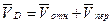по теореме Вариньона,

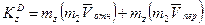. (14)

Но вектор 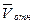лежит в одной плоскости с осью z и, следовательно, 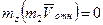. Вектор 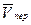направлен перпендикулярно плите (как ось Х, если осьь Y в плоскости плиты); по модулю 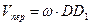. Тогда 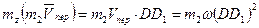. Но из рис. Д2в видно, что DD₁ =l + l sin φ. Взяв значение sin φ из формулы (3) и подставив все найденные величины в равенство (14), получим

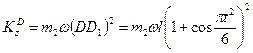. (15)

Зная 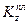и 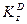[формулы (13) и (15)], найдем из равенства (12) значение Kz., тогда уравнение (11) примет вид

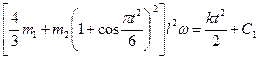. (16)

или при числовых значениях задачи

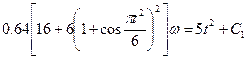
Постоянную интегрирования определим по начальным условиям: при t = 0 ω = ω₀ = 5 с^-1 ; получим С₁ = 128. При этом значении С, из уравнения (16) находим искомую зависимость ω от t.

Ответ:

.

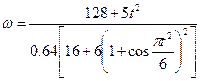Примечание. Из полученного результата можно найти и значение ω₁ при t = t₁. Но если по условиям задачи одновременно М = 0, то уравнение (10) дает Кz = const, и тогда обычно проще не искать зависимость ω от t в общем виде, а сначала определить положение груза D npu t = 0 (т.е. угол φ₀ ) и вычислить значение Kzo при φ = φ₀ и ω =ω₀ с помощью равенств, аналогичных (11) — (15); затем определить положение груза при t = t₁ (угол φ₁) и тем же путем найти Kz₁ при φ = φ₁ и ω = ω₁. Так, в рассмотренном примере при t = 0 будет φ₀ = π/2 и DD₁ = 2l (рис Д2в),а при t = t₁ = 2 с будет φ₁ = — π/6 и DD₁ =l/2. Тогда

, .

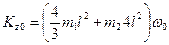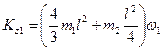Значение ω₁ находится из равенства Kz₁ = Кzо.

Задача Д3

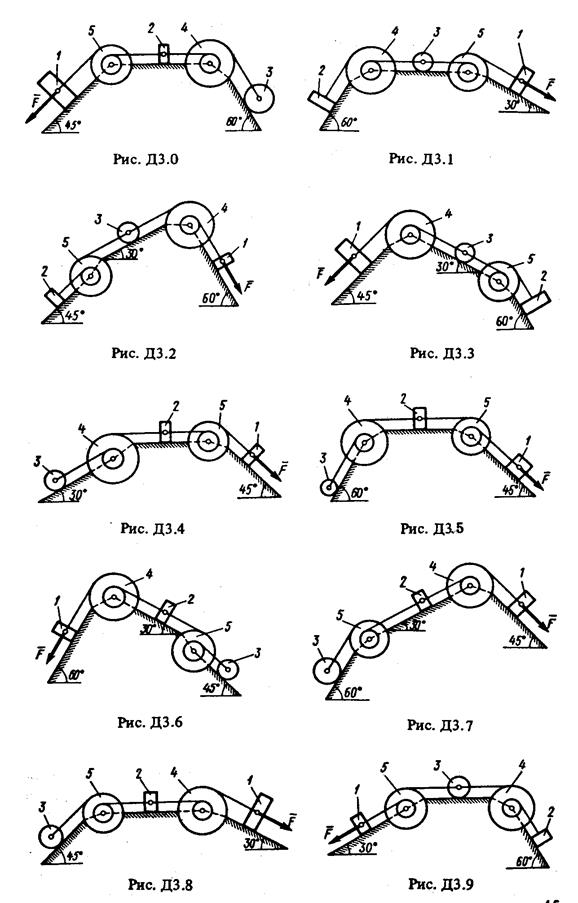
Механическая система состоит из грузов 1 и 2 (коэффициент трения грузов о плоскость f = 0,1), цилиндрического сплошного однородного катка 3 и ступенчатых шкивов 4 и 5 с радиусами ступеней R₄ = 0,3 м, г₄ = 0,1 м, R_s = 0,2 м, r_s = 0,1 м (массу каждого шкива считать равномерно распределенной по его внешнему ободу) (рис. ДЗ.О-Д3.9, табл. ДЗ). Тела системы соединены друг с другом нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям

Таблица ДЗ

Номер условия	m1 кг	m2 кг	m3 кг	m4 кг	m5 кг	M4 Н*м	M5 Н*м	F = f(f), Н	S1 м	Найти
							0,8	50(2+ 3s)	1,0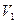
						0,6		20(5 + 2s)	1,2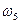
							0,4	80(3 + 4s)	0,8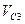
						0,3		40(4 + 5i)	0,6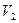
							0,6	30(3 + 2s)	1,4
						0,9		40(3 + 5s)	1,6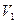
							0,8	60(2 + 5s)	1,0
						0,6		30(8 + 3s)	0,8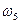
						0,3		40(2 + 5s)	1,6
							0,4	50(3 + 2s)	1,4

Под действием силы F = f (s) , зависящей от перемещении точки приложения силы, система приходит в движение из состояния покоя. При движении системы на шкивы 4 и 5 действуют постоянные моменты сил сопротивлений, равные соответственно M₄ и M_s,

Определить значение искомой величины в тот момент времени, когда перемещение точки приложения силы 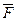равно s₁. Искомая величина указана в столбце "Найти" таблицы, где обозначено: V₁ - скорость груза 1, V_C3 - скорость центра масс катка 3, ω₄ - угловая скорость тела 4 и т.д.

Указания. Задача ДЗ - на применение теоремы об изменении кинетической энергии системы. При решении задачи учесть, что кинетическая энергия системы равна сумме кинетических энергий всех входящих в систему тел: эту энергию нужно выразить через ту скорость (линейную или угловую), которую в задаче надо определить. П0440и вычислении кинетической энергии катка, движущегося плоскопараллельно, для установления зависимости между его угловой скоростью и скоростью его центра масс воспользоваться понятием о мгновенном центре скоростей (кинематика). При определении работы все перемещения следует выразить через заданное перемещение s₁, учтя, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями.

Когда по данным таблицы m₂ = 0, груз 2 на чертеже не изображать; шкивы 4 и 5 всегда входят в систему.

Пример ДЗ. Механическая система (рис, ДЗ) состоит из сплошного цилиндрического катка /, ступенчатого шкива 2 с радиусами ступеней R₂ и r₂ (масса шкива равномерно распределена по его внешнему ободу) и груза 3 (коэффициент трения груза о плоскость равен f). Тела системы соединены друг с другом нитями, намотанными на шкив 2.

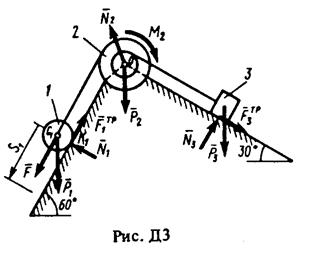
Под действием силы F = зависящей от перемещения s точки ее приложения, система приходит в движения из состояния покоя. При движении на шкив 2 действует постоянный момент М₂ сил сопротивления.

Дано: m₁ = 4 кг, m₂ = 10кг, m₃ = 8 кг. R₂ = 0,2 м, r₂ = 0,1 м, f = 0,2, М₂ = 0,6 Н • м, F = = 2(1 + 2s) Н, s_l = 2м,

Определить: скорость V_C1 центра масс катка, когда s = s₁

Решение. 1. Рассмотрим движение неизменяемой механической системы, состоящей из теп 1, 2. 3, соединенных нитями. Изобразим все действующие на систему внешние силы: активные 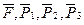, момент сопротивления М₂, реакции 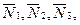и силы трения 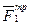и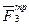

Для определения V_C1 воспользуемся теоремой об изменении кине­тической энергии системы

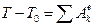. (1)

2. Определяем Т₀ и Т. Так как в начальный момент система находи­лась в покое, то Т₀ = 0. Величина T равна сумме энергий всех тел системы:

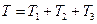(2)

Учитывая, что тело 1 движется плоскопараллельно, тело 3 - поступательно, а тело 2 вращается вокруг неподвижной оси, получим

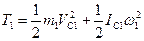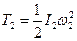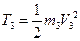, , (3)

Все входящие сюда скорости следует выразить через искомую V_C1. Приняв во внимание, что точка K₁ - мгновенный центр скоростей катка 1, и обозначив радиус катка через г₁, получим

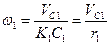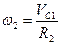
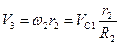, . (4)

Кроме того, входящие в (3) моменты инерции имеют значения

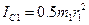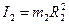, (5)

Подставив все величины (4) и (5) в равенство (3), а затем используя равенство (2), получим окончательно:

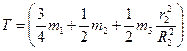
3. Теперь найдем сумму работ всех действующих внешних сил при том перемещении, которое будет иметь система, когда точка С₁ пройдет путь s . Одновременно все перемещения следует выразить через заданную величину s₁ , для чего учтем, что здесь зависимость между перемещениями будет такой же. как и между соответствующими скоростями в равенствах (4). т.е. 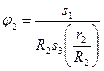В результате получим:

, ,

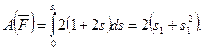
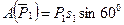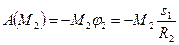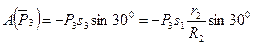
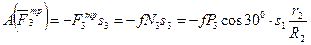
Работа остальных сил равна нулю, так как точка К₁, где приложе­ны 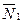, и 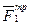- мгновенный центр скоростей, точка О. где приложены 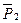и 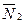. неподвижна, а реакция 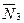, перпендикулярна перемещению груза 3. Тогда окончательно

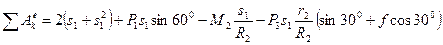(7)

4. Подставив выражения (6) и (7) в уравнение (I) и учитывая, что T₀ = 0, получим

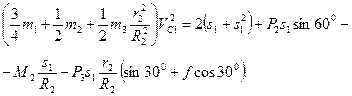(8)

При числовых значениях, которые имеют заданные величины, равенство (8) дает 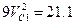. Отсюда находим искомую скорость. Ответ; 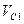= 1,53 м/с.