Метод Гаусса- Зайделя.
Пусть мы имеем зависимость давления от температуры Р=f(T).
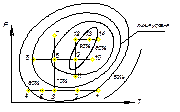
1-14 – серии опытов и выбранных точек.
Копт=f(Р,Т)
Линии уровня определяют выход продукта, %.
1). Проводится серия опытов при постоянном давлении (1,2,3,4) наилучший результат 3.
2). При постоянной температуре в точке (3) проводится следующая серия опытов (5,6,7).
Меняется давление, наилучший результат (6).
3). Аналогично проводятся следующие серии опытов при фиксированном каком-то параметре. Это позволяет определить max выход продукта.
Предпочтение отдают значению Копт. При меньших значениях параметров. В данном случае опыту (9), а не (13).
Метод Бокса –Уилсона.
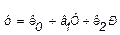 (1)
(1)
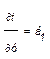 (3)
(3) 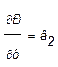 (4)
(4)
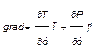 (2)
(2)
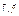 - орты, направленные вдоль координатных осей и равные по величине.
- орты, направленные вдоль координатных осей и равные по величине.
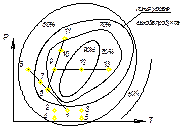
1). Проводится опыт (1) с близкими значениями Р и Т к этому опыту проводятся опыты (2,3,4,5). В координатных осях они охватывают плоскость, которую можно описать ур-ем (1) , взяв grad этой функции (1) получим (2) ур-е можно определить направление возрастания функции.
Grad – это вектор, показывающий в каком направлении функция возрастает с наибольшей скоростью.
По ур-ю (1) и (2) с учётом (3) и (4) можно определить это направление.
2). В направлении возрастающей функции проводятся опыты (6,7,8), наилучший (6). В окрестности этой точки проводится ещё четыре опыта для математического описания ур-я (1). Порядок определяется наибольшего возрастания функции, аналогичен первому пункту.
3). При окончательном определении экстремум функции max используют описание плоскости уже полиномом.
Дата добавления: 2015-06-17; просмотров: 680;
