Общий вид математического описания РИВ.

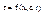
Для вывода конкретного уравнения РИВ используют уравнение материального баланса

(1)

Тип реакции A R

При стационарном режиме в РИВе

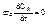; ; Д=0

Тогда уравнение (1) примет вид

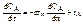(2) - нестационарный режим

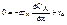(3) - стационарный режим

Из (3) находим математическое описание РИВ

; ;

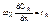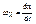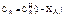
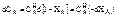
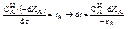(4)

Уравнение (4) интегрируем в пределах измерения во времени от 0 до τ и степени превращения от 0 до Х_А.

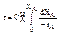(5)

таким образом математические описания РИВ и ПРИС одинаковые.

Различие_________ для ПРИС уравнеие получено (для нестационарного режима), а для РИВ (стационарный режим).

Определим уравнение для РИВ при порядке реакции n=n; n=1; n=0;

Известно, что 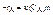(6), а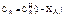

Подставим уравнение (6) и (7) в (5)

(8) при n=n;

n=1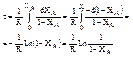

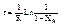(9) при n=1

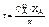(10) при n=0

Если начальная степень превращения реагента А и 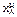не равны нулю то уравнения (9) и (10) приму вид

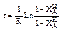(11) при n=1

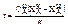(12) при n=0

При порядке реакции n не равно нулю и n не равно единице, уравнение (8) трудно интегрировать, поэтому применяют метод графического интегрирования.

рис 1

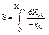1- ; 2- ;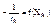

1) Строятся графическая зависимость в координатах 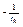и Х_А т.е.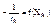

2) Определяется площадь под кривой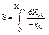

3) Произведение концентрации 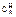на S даёт возможность определить площадь химического процесса.