Периодический реактор идеального смешения (ПРИС)
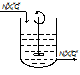
В ПРИСе за счет идеального перемешивания параметры и концентрация реагентов постоянны в какой-то момент времени.
Графически:
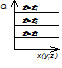
t-время
x(y;z)-пространственные координаты
СА-концентрация реагента А
Но параметры и концентрация реагентов в ПРИСе изменяются во времени.
Графически:
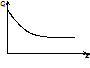
Общий вид математического описания ПРИСа
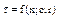
Где: x-степень превращения исходного реагента
С-концентрация исходного реагента
r-скорость реакции
Конкретный вид математ. описания ПРИСа определяется из уравнения материального баланса.
Для элементарного объема реактора по изменению реагента А материальный баланс представляется в виде ; A  R
R
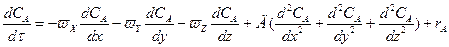
I. Изменение реагента А в объеме аппарата за счет скорости по осям
II. Изменение реагента А за счет молекулярной и конвективной диффузии по осям x, y,z
III. Изменение реагента А за счет скорости химической реакции
wx, wy, wz - скорости среды по осям x,y,z
Д – коэффициент молекулярной и конвективной диффузии
ra- скорость химической реакции
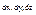 и
и 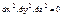
Периодический процесс в реакторе это не стационарный процесс и он характеризуется изменением концентрации. 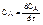
При идеальном перемешивании концентрация реагента остается постоянной по всем осям x, y,z. Поэтому :
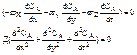
Тогда 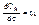 или
или 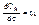 (1)
(1)
Известно, что
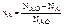 (2)
(2)
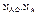 - количество вещества А в начале и в конце реакции ( Na- текущая концентрация)
- количество вещества А в начале и в конце реакции ( Na- текущая концентрация)
Если реакционный объем Vр =const, то
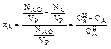 (3)
(3)
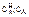 - начальная и текущая концентрация реагента А
- начальная и текущая концентрация реагента А
Из уравнения (3) определяем текущую концентрацию Са
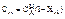 (4)
(4)
Скорость химической реакции в общем виде выражается : 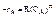 (5)
(5)
Производная от уравнения( 4)
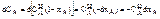 (6)
(6)
С учетом уравнений (5) и (6) уравнение (1) будет : 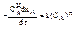
Если уравнение( 6) поставить в уравнение (1), то получим математическое описание ПРИСа 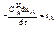 или
или 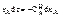
Или 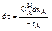 (7)
(7)
Проинтегрировав уравнение (7) в пределах изменения времени пребывания от 0 до t и степени превращения от 0 до Xа получим
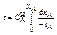 (8)
(8)
Это и есть модель ПРИСа или математическое описание ПРИСа (времени реакции)
Математическое описание ПРИСа при порядке реакции n=n
Уравнение (4) и (5) подставим в уравнение (8)
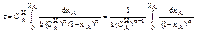
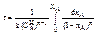 (9) при n=n
(9) при n=n
При порядке реакции n=1
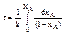 (10)
(10)
При порядке реакции n=0
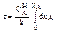 (11)
(11)
Уравнение (10) и (11) проинтегрируем
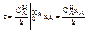
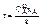 (12) n=0
(12) n=0
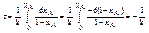 ln
ln 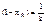 ln
ln 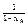
 ln
ln 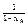 (13) n=1
(13) n=1
Если начальная степень превращения 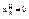 , то уравнения 9, 12,13 примут вид
, то уравнения 9, 12,13 примут вид
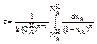 (14) n=n
(14) n=n
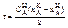 (15) n=0
(15) n=0
 ln
ln  (16) n=1
(16) n=1
Если порядок реакции 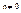 и
и 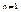 , то уравнение (9) трудно интегрировать, поэтому применяют метод графического интегрирования.
, то уравнение (9) трудно интегрировать, поэтому применяют метод графического интегрирования.
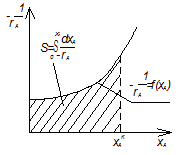
1.Строим графическую зависимость в координатах
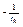 и
и 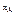 т.е.
т.е. 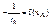
2,Находят площадь S под кривой
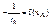 ;
; 
3.Произведение начальной концентрации 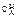 на площадь S дает время химического процесса
на площадь S дает время химического процесса
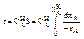
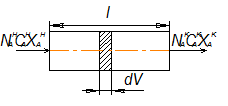
7 Реакторы идеального вытеснения (РИВ)
РИВ – трубчатый аппарат длина которого значительно превышает диаметр ( непрерывый процесс осуществляется)
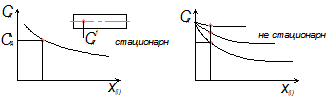
Непрерывный процесс может быть стационарным и нестационарным. Последний характерен для привода пуска и остановки РИВ.
В РИВе степень превращения 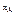 и концентрация
и концентрация 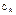 изменяются:
изменяются:
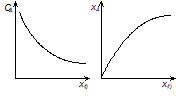
Особенности РИВ.
1.Среда движется в одном направлении по 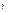 - длине
- длине
2.Продольное и поперечное перемешивание отсутствуют.
3.Среда движется как поршень не перемешиваясь с предыдущими и последующими слоями, такой режим называется поршневым..
4. Состав среды изменяется вдоль РИВ в определенной зависимости.
5.Время пребывания каждой частицы в РИВе одинаково.
Дата добавления: 2015-06-17; просмотров: 622;
