В ПРОТОЧНЫХ РЕАКТОРАХ

Важной характеристикой структуры потока в проточных реакторах является функция распределения времени пребывания. Зная функцию распределения времени пребывания, можно оценить степень отклонения реального реактора от идеальных моделей, определить параметры моделей реакторов с неидеальной структурой потока, в частности, ячеечной и диффузионной, а также решить ряд других практических задач.

Экспериментально функция распределения времени пребывания может быть найдена путем исследования так называемых кривых отклика. Суть этого метода состоит в следующем. На входе в реактор создается некоторое возмущение. Таким возмущением является введение в основной поток вещества (индикатора). К индикатору (трассеру) предъявляются следующие требования:

– индикатор по какому-либо свойству (окраске, электропроводности, радиоактивности и т.д.) должен отличаться от реакционной смеси;

– индикатор не должен взаимодействовать с реакционной смесью и оборудованием;

– индикатор должен быстро определяться.

Возмущение на вход (входной сигнал) может быть ступенчатым (до момента времени τ₀ = 0 индикатор не вводили в поток, а с момента τ₀ его вводят в постоянном количестве), импульсным (мгновенное введение порции индикатора) или периодическим (например, иметь синусоидальный характер). Для получения кривой отклика на входной сигнал в разные моменты времени измеряют концентрацию или количество индикатора в потоке, выходящем из реактора (рисунки 12.1, 12.2, 12.3).

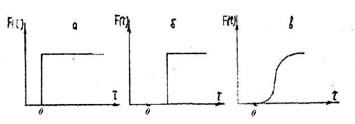
а – на входе в реактор; б – на выходе из РИВ; в – на выходе из

реального реактора при наличии продольного перемешивания

Рисунок 12.1 – Кривые отклика при ступенчатом

вводе индикатора

а – на входе в реактор; б – на выходе из РИВ; в – на выходе из

реального реактора при наличии продольного перемешивания

Рисунок 12.2 – Кривые отклика при импульсном вводе

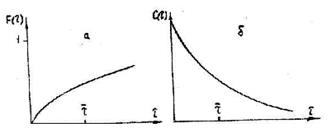
а – при ступенчатом вводе индикатора;

б – при импульсном вводе индикатора

Рисунок 12.3 – Кривые отклика в РИС-Н

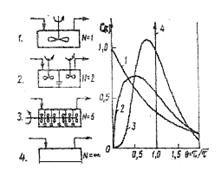Для ячеечной и однопараметрической модели построены зависимость F(r) и C(τ) от безразмерного времени (рисунки 12.4, 12.5, 12.6).

	Рисунок 12.4 – Дифференциальные функции распределения времени пребывания для ячеечной модели		Рисунок 12.5 – Интегральные функции распределения времени пребывания для ячеечной модели

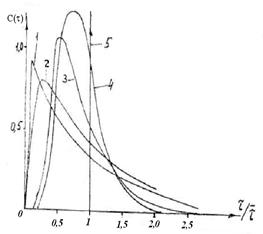
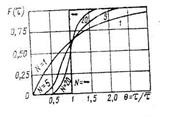
1 - P_е^/ = 0,1; 2 - P_е^/ = 1; 3- P_е^/ = 10; 4 - P_е^/ = 17,8; 5- P_е^/ = ∞:

Рисунок 12.6 – Дифференциальные функции распределения

времени пребывания для диффузионной модели при различных

значениях критерия P_е^/

Из сравнения рисунков видно, что функция распределения для ячеечной модели при N=1 практически совпадает с кривой распределения для диффузионной модели при P_e' 0, а при больших значениях N – с кривыми, для которых P_e' >> 1. Этот результат вполне естественен, так как и диффузионная, и ячеечная модели являются лишь разными приближениями одного и того же процесса.

Таким образом, если экспериментально найдена кривая отклика для реактора с реальным гидродинамическим режимом, то, сопоставив ее с расчетными кривыми, можно определить параметр модели.