Реактор идеального смешения непрерывного действия

(РИС- Н)

Для получения большого количества продуктов одинакового качества используют РИС-Н. По определению РИС-Н, работающего в стационарных условиях, в уравнении материального баланса (8.3) будет отсутствовать диффузионный перенос и накопление вещества в реакторе.

Уравнение материального баланса РИС-Н, работающего в стационарном режиме:

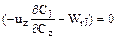, (8.9)

где u_z – проекция скорости на ось z.

Представим это уравнение в конечно-разностной форме:

; ; ; ,

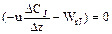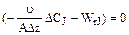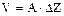где А – площадь «живого» сечения реактора;

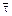– среднее время пребывания реагентов в проточном реакторе.

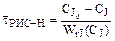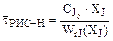и . (8.10)

Эти уравнения материального баланса можно использовать не только для определения среднего времени пребывания 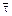и затем размеров реакционного пространства при заданной глубине химического превращения, но и для решения обратной задачи: при заданном объеме реактора и заданной производительности по исходному реагенту определить концентрацию на выходе из реактора.

Рассмотрим простую необратимую реакцию первого порядка

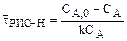и 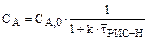. (8.11)

Зачастую скорость сложных реакций с невыясненным до конца механизмом выражают в виде кинетических уравнений дробного порядка. В этом случае аналитическое решение оказывается невозможным, и приходится прибегать к численным методам расчета:

. (8.12)

Преобразуем уравнение:

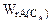
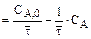. (8.13)

Полученное уравнение состоит из двух частей: слева – кинетическое уравнение, которое можно определить по закону действующих масс, а справа – уравнение прямой линии, где угловой коэффициент равен (-1/ 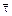). Построив кривую и прямую в координатах W_rA – C_A, получим точку пересечения М, которая позволяет определить концентрацию С_А на выходе из реактора (рисунок 8.11).

Рисунок 8.11 – Графический метод определения концентрации

реагента на выходе из РИС-Н

9 РЕАКТОР ИДЕАЛЬНОГО ВЫТЕСНЕНИЯ.

СРАВНЕНИЕ ПРОТОЧНЫХ РЕАКТОРОВ

РИВ представляет собой длинный канал, через который реакционная смесь движется в поршневом режиме. Каждый элемент потока условно выделяется двумя плоскостями, перпендикулярными оси канала, движется через него как твердый поршень, вытесняя предыдущие элементы потока и не перемешиваясь ни с предыдущими, ни со следующими за ним элементами (рисунки 9.1, 9.2).

Идеальное вытеснение возможно при выполнении следующих допущений:

- движущийся поток имеет плоский профиль линейных скоростей;

- отсутствует обусловленное любыми причинами перемешивание в направлении оси потока;

- в каждом отдельно взятом сечении, перпендикулярном оси потока, параметры процесса (концентрации, температуры и т.д.) полностью выравнены.

Следует отметить, что строго эти допущения в реальных аппаратах не выполняются. Из гидравлики известно, что даже в очень гладких каналах при движении потока, характеризующегося высокими числами Рейнольдса, у стенок канала существуют так называемый пограничный, вязкий подслой, в котором градиент линейной скорости очень велик. Максимально приблизиться к идеальному вытеснению можно лишь в развитом турбулентном режиме. Примерами РИВ являются абсорберы, десорберы, башни с насадкой и орошением.

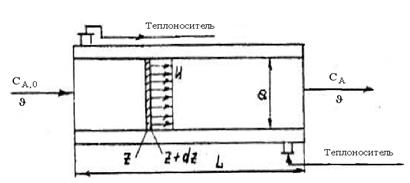
Рисунок 9.1 – Схематическое изображение РИВ

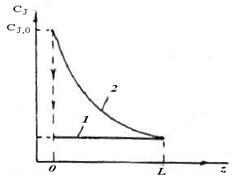
Рисунок 9.2 – Распределение вдоль оси реактора концентрации

исходного реагента в РИС-Н (1) и РИВ (2)

Из определения РИВ следует, что в реакторе отсутствует диффузионный перенос:

(-U_Z 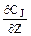– W_rJ ) = 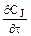. (9.1)

Если реактор работает в стационарном режиме, то отсутствует накопление вещества в реакторе:

(-U_Z 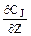– W_rJ)= 0 . (9.2)

Принимаем V/n= 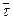. Если площадь «живого» сечения реактора постоянная, то

U_Z = , (9.3)

где А – площадь «живого» сечения.

После преобразований и интегрирования получаем

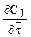– – W_rJ = 0. (9.4)

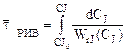и 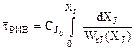. (9.5)

Получили выражения, аналогичные РИС-П (отличие: для РИВ –среднее время пребывания частиц 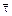, а для РИС-П – физическое время ).

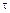В РИВ концентрация выше, чем в РИС-Н, следовательно, больше скорость химической реакции. Если условия проведения реакции 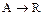одинаковые, то можно сравнить эффективность РИВ и РИС-Н графически.

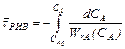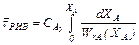; ; (9.6)

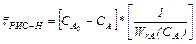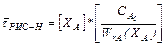; . (9.7)

В координатах 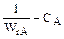и

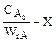
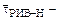площадь под криволинейной трапецией;

площадь прямоугольника (рисунок 9.3).

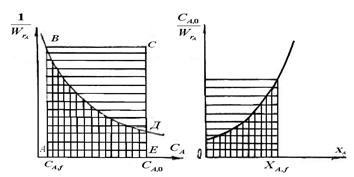
Рисунок 9.3 – Графическое сравнение проточных реакторов

идеального смешения и вытеснения как площадей

геометрических фигур

На практике не всегда стремятся к поддержанию более высоких концентраций исходных реагентов (т.е. малому объему реактора). При проведении параллельных реакций разного порядка в том случае, если порядок целевой реакции меньше порядка побочной реакции (n₁ <n₂), при низких концентрациях исходных реагентов обеспечиваются более высокие значения дифференциальной селективности.

Сравним РИС-Н и РИВ при проведении параллельных реакций разного порядка по выходу целевого продукта.

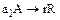и 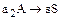. (9.8)

Допущения: 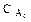; ; 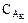; 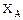V= const; 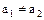; 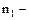порядок целевой реакции; порядок побочной реакции.

Для удобства дальнейшего рассмотрения представим систему стехиометрических уравнений (9.8) в эквивалентном виде:

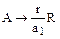и .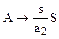

Выход целевого продукта определим по формуле

. (9.9)

Достигаемая на выходе из реактора концентрация С_R будет определяться, с одной стороны, выбранным типом реактора, а с другой – кинетическими особенностями реакций, которые могут быть учтены через дифференциальную селективность:

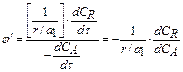. (9.10)

Проинтегрируем дифференциальное уравнение и получим зависимость концентрации С_R от дифференциальной селективности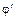

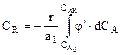. (9.11)

Подставим значение С_R в уравнение выхода продукта (9.9)

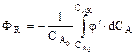. (9.12)

Дифференциальная селективность 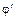, стоящая под знаком интеграла, является в общем случае убывающей или возрастающей функцией концентрации исходного реагента А.

По определению РИС-Н С_А=const, следовательно,

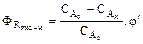, (9.13)

а для РИВ концентрация С_А изменяется:

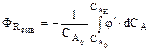. (9.14)

В координатах 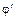– 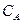выход продукта в РИС-Н представляет площадь прямоугольника, а в РИВ – площадь под криволинейной трапецией. Соотношение между этими площадями зависит от характера функции 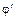( 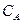) (рисунок 9.4).

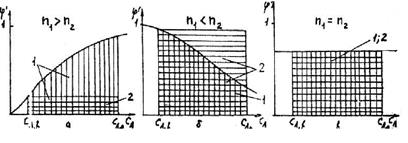
Рисунок 9.4 – Графическое сравнение выхода целевого продукта

в проточных реакторах идеального вытеснения 1

и идеального смешения 2 при проведении

параллельных реакций разного порядка: а) для n₁ > n₂;

б) для n₁ < n₂; в) для n₁ = n₂

По условию , :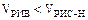

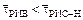1) если 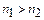, то ;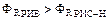

2) если , то ;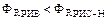

3) если , то .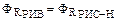

Сравнивая проточные реакторы, можно сделать следующие выводы:

1) иногда выгоднее применять РИВ, а иногда РИС-Н;

2) при проведении реакции в одинаковых условиях ;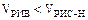

3) при проведении одной и той же реакции в одинаковых условиях реакторы РИВ имеют большее гидравлическое сопротивление (выше эксплуатационные затраты);

4) РИВ значительно труднее чистить;

5) РИС-Н проще конструктивно, но из-за малой концентрации реагентов у них малая скорость химической реакции. Для устранения недостатков РИС-Н используют каскад РИС (К-РИС).