Совместное решение материального и теплового

балансов для стационарного адиабатического реактора РИС–Н

Математическая модель адиабатического реактора РИС-Н

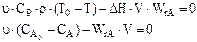. (13.17)

Система уравнений материального и теплового балансов представляет собой математическую модель реактора.

Определим значения степени превращения X_А и температуры Т, достигаемые в реакторе. Естественно, что частные значения будут зависеть от конкретного вида кинетического уравнения. Скорость химической реакции зависит от концентрации C_A и температуры T.

Рассмотрим самые простые варианты:

– необратимую реакцию первого порядка А 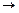R;

– обратимую реакцию первого порядка А 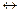R.

Предварительно преобразуем математическую модель реактора.

Ранее (см. раздел 2) получено:

. (13.18)

Уберем скорость химической реакции из уравнения теплового баланса (13.17). Представим произведение скорости химической реакции на объем, как

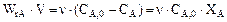. (13.19)

Тогда уравнение теплового баланса будет:

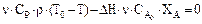. (13.20)

Математическую модель реактора можно представить следующим образом:

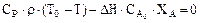; (13.21)

.

Для необратимой реакции первого порядка скорость химической реакции

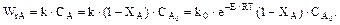.(13.22)

Подставив значение скорости химической реакции в математическую модель реактора (13.21), получим систему уравнений:

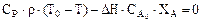. (13.23)

Аналитическое решение системы уравнений (13.23) затруднено, т.к. температура Т входит в уравнения в виде линейного члена и в составе комплекса. Для решения используем численные методы, т.к. уравнения являются трансцендентными.

Решим систему графическим методом.

Уравнение теплового баланса (13.23) преобразуем и получим:

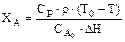. (13.24)

В координатах X_A-Т это уравнение прямой линии, где отрезок, отсекаемый на оси абсцисс – начальная температура Т₀. Наклон линии будет определять значение изменения энтальпии 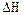. Крутизну угла наклона можно изменить, меняя начальную концентрацию 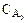(рисунок 13.1).

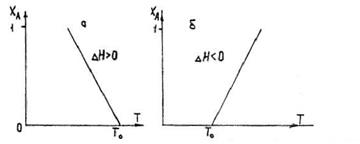
Рисунок 13.1 – Уравнение теплового баланса

реактора идеального смешения для эндотермических (а)

и экзотермических реакций (б)

Преобразуем зависимость:

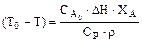. (13.25)

Принимаем, что степень превращения X_A = 1, следовательно,

. (13.26)

Величина ΔТ_адиаб. показывает максимальное изменение температуры реакционной смеси, возможное в адиабатических условиях

. (13.27)

Для необратимой простой реакции

. (13.28)

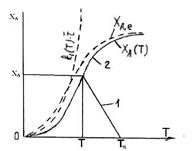
Решение системы уравнений материального и теплового балансов имеет различный вид для экзо- и эндотермических реакций (рисунки 13.2, 13.3).

Для эндотермической реакции возможно только одно решение, в то время как для экзотермической реакции, в зависимости от начальных температур Т₀₁,Т₀₂,Т₀₃, возможно от одного до трех решений.

Если обратимая простая реакция, то

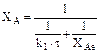. (13.29)

Для обратимой реакции степень превращения Х_А фактически будет находиться ниже равновесной кривой, следовательно, для эндотермической реакции одно решение, а для экзотермической в зависимости от начальной температуры Т₀, будет от одного до трех решений (рисунки 13.4, 13.5).