ПОСЛЕДОВАТЕЛЬНЫЙ КОЛЕБАТЕЛЬНЫЙ
КОНТУР
4.1. Схема последовательного колебательного контура

 Последовательным колебательным контуром называют электрическую цепь, представляющую собой последовательное соединение катушки индуктивности и конденсатора. Его возможные варианты включения как четырехполюсника показа- ны на рис. 4.1 (выход-
Последовательным колебательным контуром называют электрическую цепь, представляющую собой последовательное соединение катушки индуктивности и конденсатора. Его возможные варианты включения как четырехполюсника показа- ны на рис. 4.1 (выход-
ное напряжение сни- Рис. 4.1
мается с конденсатора
или с катушки индуктивности).
Конденсатор и катушка индуктивности имеют внутренние потери энергии, которые учитываются последовательно соединенными с ними эквивалентными сопротивлениями потерь 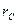 и
и 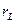 соответственно. На практике в керамических конденсаторах всегда
соответственно. На практике в керамических конденсаторах всегда 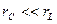 и потерями в них пренебрегают, тогда эквивалентные схемы последовательных колебательных контуров рис. 4.1 примут вид, показанный на рис. 4.2.
и потерями в них пренебрегают, тогда эквивалентные схемы последовательных колебательных контуров рис. 4.1 примут вид, показанный на рис. 4.2.
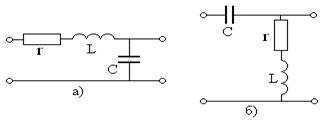
Рис. 4.2
В дальнейшем будем рассматривать схему на рис. 4.2а, в которой выходное напряжение снимается с емкости, а схему
на рис. 4.2б аналогично рассмотрите самостоятельно.
4.2. Входное сопротивление последовательного
колебательного контура
Определим входное сопротивление последовательного колебательного контура показанного на рис. 4.3. Полное комплексное сопротивление 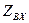 равно
равно
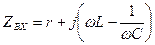 . (4.1)
. (4.1)
Рис. 4.3 Его модуль 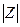 , аргумент
, аргумент 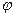 , активная
, активная
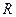 и реактивная
и реактивная 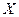 составляющие соответственно равны:
составляющие соответственно равны:
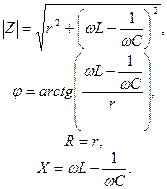
Зависимости этих функций от частоты сигнала при 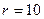 Ом,
Ом, 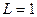 мГн,
мГн, 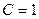 нФ показаны на рис. 4.4. На частоте
нФ показаны на рис. 4.4. На частоте
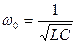 (4.2)
(4.2)
реактивное сопротивление 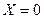 и
и 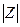 принимает минималь-
принимает минималь-
ное значение, равное 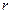 ,
,
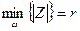 . (4.3)
. (4.3)
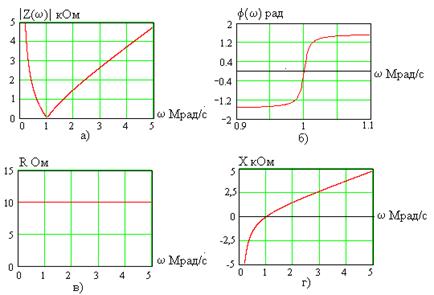
Рис. 4.4
При отклонении частоты от 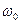 модуль сопротивления контура резко возрастает. В области
модуль сопротивления контура резко возрастает. В области 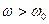 реактивное сопротивление положительно, то есть контур имеет индуктивный характер сопротивления, сдвиг фаз между напряжением и током
реактивное сопротивление положительно, то есть контур имеет индуктивный характер сопротивления, сдвиг фаз между напряжением и током 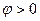 . В области
. В области 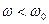 реактивное сопротивление отрицательно и сопротивление контура имеетемкостный характер
реактивное сопротивление отрицательно и сопротивление контура имеетемкостный характер 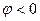 .
.
4.3. Ток и напряжения в контуре, резонансные явления
Подключим к контуру рис. 4.2а идеальный источник гармонического напряжения, получим схему на рис. 4.5.
 Комплексная амплитуда ЭДС источника равна
Комплексная амплитуда ЭДС источника равна 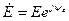 , тогда для комплексной амплитуды тока в контуре получим
, тогда для комплексной амплитуды тока в контуре получим
Рис. 4.5 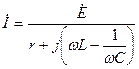 , (4.4)
, (4.4)
а для его амплитуды 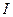 и начальной фазы
и начальной фазы 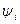 соответственно
соответственно
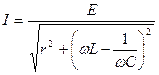 , (4.5)
, (4.5)
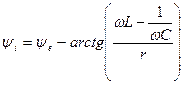 . (4.6)
. (4.6)
Зависимости амплитуды и начальной фазы тока от частоты при 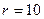 Ом,
Ом, 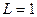 мГн,
мГн, 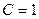 нФ,
нФ, 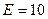 В и
В и 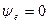 представлены на рис. 4.6.
представлены на рис. 4.6.
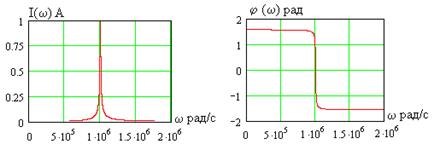
Рис. 4.6
Ток в контуре резко нарастает при приближении частоты источника к частоте 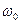 (4.3), его максимальное значение равно
(4.3), его максимальное значение равно
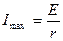 . (4.7)
. (4.7)
Однако резонанс тока в последовательном колебательном контуре отсутствует, так как ток в контуре равен току источника, а не возрастает по сравнению с ним.
Так как изменения тока происходят в малой окрестности около частоты 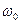 , то целесообразно строить графики в координатах абсолютной расстройки, равной
, то целесообразно строить графики в координатах абсолютной расстройки, равной
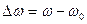 , (4.8)
, (4.8)
то есть производится смещение начала координат в точку 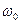 .
.
Те же графики, что и на рис. 4.6, но в координатах 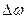 , показаны на рис. 4.7.
, показаны на рис. 4.7.
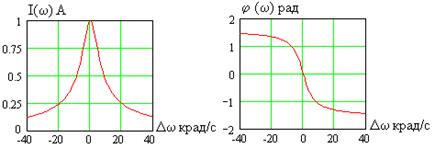
Рис.4.7
Как видно, координаты абсолютной расстройки удобны для построения графиков частотных характеристик колебательного контура.
Определим комплексные амплитуды напряжений на элементах контура:
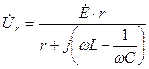 , (4.9)
, (4.9)
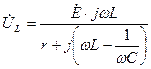 , (4.10)
, (4.10)
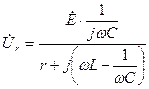 . (4.11)
. (4.11)
Тогда для амплитуд этих напряжений получим:
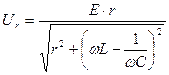 , (4.12)
, (4.12)
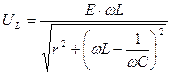 , (4.13)
, (4.13)
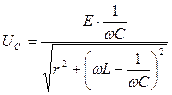 . (4.14)
. (4.14)
а их начальные фазы равны
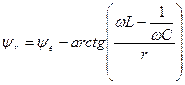 , (4.15)
, (4.15)
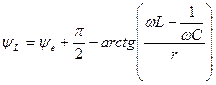 , (4.16)
, (4.16)
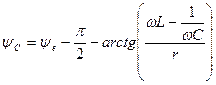 . (4.17)
. (4.17)
На рис. 4.8 показаны зависимости амплитуд напряжений на элементах контура при 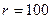 Ом,
Ом, 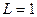 мГн,
мГн, 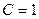 нФ,
нФ, 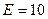 В и
В и 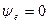 (обратите внимание, что сопротивление потерь в 10 раз больше, чем в предыдущем примере)
(обратите внимание, что сопротивление потерь в 10 раз больше, чем в предыдущем примере)
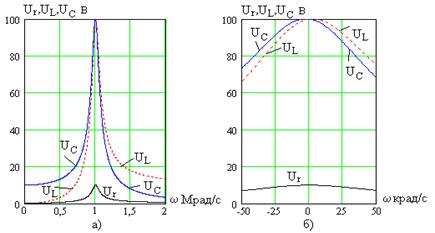
Рис. 4.8
На рис. 4.8а кривые представлены в широком диапазоне частот, а на рис. 4.8б – в координатах абсолютной расстройки и узком частотном интервале в окрестности 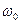 .
.
Как видно на частоте 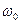 напряжения на индуктивности и емкости резко возрастают по сравнению с напряжением (ЭДС) источника (становятся много больше
напряжения на индуктивности и емкости резко возрастают по сравнению с напряжением (ЭДС) источника (становятся много больше 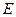 ), то есть в последовательном колебательном контуре имеет место резонанс напряжений на реактивных элементах. Напряжение на сопротивлении
), то есть в последовательном колебательном контуре имеет место резонанс напряжений на реактивных элементах. Напряжение на сопротивлении 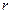 не превышает входной ЭДС, поэтому о его резонансе говорить не приходится.
не превышает входной ЭДС, поэтому о его резонансе говорить не приходится.
Частоты, на которых напряжения 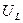 и
и 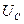 максимальны, примерно равны
максимальны, примерно равны 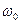 , поэтому частоту (4.2)
, поэтому частоту (4.2)
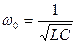
называют резонансной.
Точные значения резонансных частот нетрудно найти, определив производные 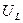 и
и 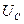 по частоте
по частоте 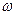 и приравняв результат нулю (проделайте это самостоятельно). Как видно из кривых рис. 4.8б, эти частоты отличаются от
и приравняв результат нулю (проделайте это самостоятельно). Как видно из кривых рис. 4.8б, эти частоты отличаются от 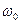 весьма незначительно (резонансная частота напряжения емкости меньше
весьма незначительно (резонансная частота напряжения емкости меньше 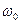 , а индуктивности – больше) и тем сильнее, чем больше сопротивление
, а индуктивности – больше) и тем сильнее, чем больше сопротивление 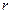 (для того, чтобы это увидеть графически и было выбрано
(для того, чтобы это увидеть графически и было выбрано 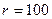 Ом).
Ом).
Принимая резонансную частоту равной 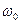 , определим резонансные амплитуды напряжений,
, определим резонансные амплитуды напряжений,
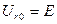 , (4.18)
, (4.18)
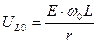 , (4.19)
, (4.19)
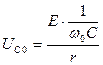 . (4.20)
. (4.20)
Подстановкой 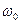 нетрудно убедиться, что
нетрудно убедиться, что
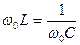 , (4.21)
, (4.21)
тогда резонансные напряжения на реактивных элементах одинаковы и равны
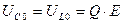 . (4.22)
. (4.22)
Величину
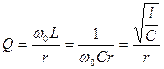 (4.23)
(4.23)
называют добротностью колебательного контура. Согласно (4.22) добротность является важнейшей характеристикой резонансных явлений.
На рис. 4.9 приведены зависимости от частоты сдвигов фаз напряжений на элементах контура относительно фазы ЭДС источника,
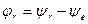 ,
,
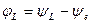 , (4.24)
, (4.24)
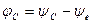 ,
,
начальные фазы напряжений определяются из (4.15)-(4.17). Как видно, напряжение на индуктивности опережает по фазе
напряжение на сопротивлении на 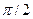 , а на емкости – отстает от него на
, а на емкости – отстает от него на 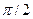 . Напряжение на индуктивности
. Напряжение на индуктивности 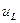 опережает по фазе напряжение на емкости
опережает по фазе напряжение на емкости 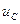 на
на 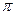 , то есть эти напряжения противофазны.
, то есть эти напряжения противофазны.
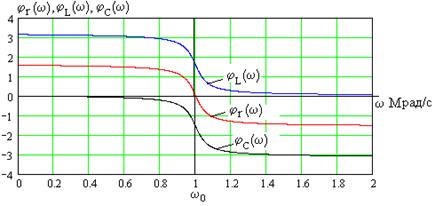
Рис. 4.9
4.4. Вторичные параметры колебательного контура
Последовательный колебательный контур полностью описывается своими первичными параметрами 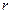 ,
, 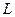 и
и 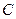 . Однако их численные значения малоинформативны, и на практике широко используются дополнительные (вторичные) параметры.
. Однако их численные значения малоинформативны, и на практике широко используются дополнительные (вторичные) параметры.
Резонансная частота контура
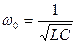 (4.25)
(4.25)
измеряется в радианах делить на секунду, или
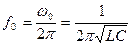 , (4.26)
, (4.26)
которая измеряется в герцах. Ее значение сразу определяет частоту настройки колебательного контура.
Характеристическое сопротивление контура
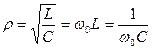 (4.27)
(4.27)
измеряется в Омах и численно равно модулю реактивного сопротивления индуктивности или емкости (отдельно) на резонансной частоте 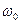 .
.
Добротность контура
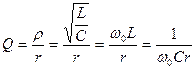 (4.28)
(4.28)
- величина безразмерная, характеризует резонансные свойства колебательного контура. Физический смысл добротности – это отношение максимальной энергии, накапливаемой в реактивных элементах, к энергии потерь в контуре за период колебаний на резонансной частоте.
Как видно из (2.28), добротность возрастает с уменьшением сопротивления потерь контура, которое практически полностью определяется потерями мощности сигнала в катушке индуктивности. На практике добротность 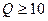 . В большинстве случаев добротность составляет 70-100. Для получения высоких добротностей 150-300 используют специальный провод (покрытый тонким слоем серебра – «серебрянку»), вжигание серебряного проводника в керамический каркас и ряд других инженерных решений. Более высокие значения добротности LC колебательных контуров получить не удается.
. В большинстве случаев добротность составляет 70-100. Для получения высоких добротностей 150-300 используют специальный провод (покрытый тонким слоем серебра – «серебрянку»), вжигание серебряного проводника в керамический каркас и ряд других инженерных решений. Более высокие значения добротности LC колебательных контуров получить не удается.
Явление резонанса и понятие добротности используются и в механических колебательных системах. Например,
в кристаллах кварца (горного хрусталя) очень малы потери энергии механических колебаний, то есть они имеют высокую добротность. Поэтому изготовленные из него бокалы при слабом ударе издают продолжительный звон. В железе, алюминии или пластмассе эти потери велики, поэтому сделанные их них бокалы не обладают соответствующим звучанием.
Помимо малых потерь энергии механических колебаний монокристаллы кварца характеризуются явлением пьезоэффекта (повторите материал по физике): при возникновении в кварцевой пластине механических колебаний на ее гранях возникает переменное напряжение и наоборот, приложенное к кристаллу переменное напряжение вызывает механические колебания кристалла. Из кварцевых пластин изготавливают электронные устройства - кварцевые резонаторы. С электрической точки зрения они эквивалентны последовательному колебательному контуру с очень высокой добротностью 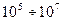 .
.
4.5. Частотные характеристики контура
Под частотными характеристиками последовательного колебательного контура (рис. 4.2) понимают зависимость от частоты характеристик комплексного коэффициента передачи по напряжению вида
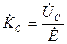 (4.29)
(4.29)
или
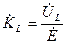 , (4.30)
, (4.30)
где 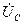 - комплексная амплитуда напряжения на емкости (обычно полагают, что потери в емкости отсутствуют),
- комплексная амплитуда напряжения на емкости (обычно полагают, что потери в емкости отсутствуют), 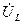 - комплексная амплитуда напряжения на последовательном со-
- комплексная амплитуда напряжения на последовательном со-
единении индуктивности 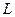 с ее сопротивлением потерь
с ее сопротивлением потерь 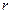 (напряжение на реальной катушке индуктивности).
(напряжение на реальной катушке индуктивности).
Рассмотрим комплексный коэффициент передачи напряжения емкости 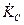 (аналогичный анализ
(аналогичный анализ 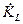 проведите самостоятельно). Из (4.29) с учетом (4.11) получим
проведите самостоятельно). Из (4.29) с учетом (4.11) получим
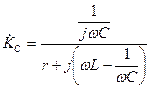 . (4.31)
. (4.31)
Из (4.31) АЧХ 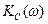 и ФЧХ
и ФЧХ 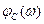 контура имеют вид
контура имеют вид
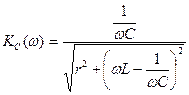 , (4.32)
, (4.32)
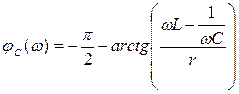 . (4.33)
. (4.33)
Частотные характеристики последовательного колебательного контура при 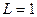 мГн,
мГн, 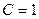 нФ для двух значений
нФ для двух значений 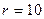 Ом (сплошные линии) и
Ом (сплошные линии) и 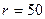 Ом (пунктир) в различных масштабах показаны на рис. 4.10 в координатах абсолютной расстройки. Кривые резко возрастает при приближении частоты сигнала
Ом (пунктир) в различных масштабах показаны на рис. 4.10 в координатах абсолютной расстройки. Кривые резко возрастает при приближении частоты сигнала 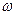 к резонансной частоте контура
к резонансной частоте контура 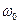 (4.25). Максимум коэффициента передачи имеет место приближенно
(4.25). Максимум коэффициента передачи имеет место приближенно
на частоте 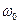 и равен добротности контура,
и равен добротности контура,
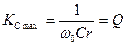 . (4.34)
. (4.34)
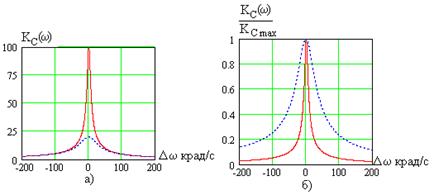
Рис. 4.10
На рис. 4.10а приведены АЧХ в абсолютном, а на рис. 4.10б в относительном масштабах по оси ординат. На рис. 4.11 показаны ФЧХ этих контуров.
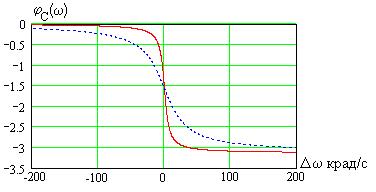
 Рис. 4.11.
Рис. 4.11.
Как видно, с ростом сопротивления потерь 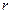 в колеба-
в колеба-
тельном контуре максимум АЧХ падает (так как уменьшается добротность) и кривая АЧХ становится «шире», а ФЧХ – более пологой.

По форме АЧХ видно, что последовательный колебательный контур является узкополосным частотным фильтром.
4.6. Обобщенная расстройка
Исследование частотных характеристик колебательного контура удобнее всего проводить в координатах обобщенной расстройки 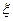 , равной
, равной
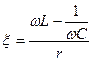 . (4.35)
. (4.35)
Как видно, она зависит от частоты сигнала и параметров контура. Проведем преобразования
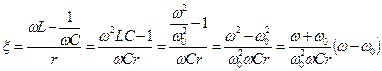 . (4.36)
. (4.36)
Обозначая абсолютную расстройку
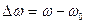 , (4.37)
, (4.37)
и приближенно полагая в первой дроби 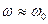 , получим
, получим
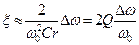 . (4.38)
. (4.38)
Из (4.38) видно, что обобщенная расстройка прямо пропорциональна абсолютной расстройке, то есть частоте сигнала (начало координат смещено в точку 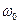 ).
).
4.7. Частотные характеристики в координатах обобщенной
расстройки
Комплексное входное сопротивление контура (4.1) в координатах 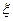 можно записать в виде
можно записать в виде
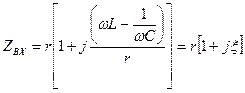 , (4.39)
, (4.39)
а его модуль, аргумент, активную и реактивную составляющие соответственно
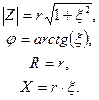 (4.40)
(4.40)
Эти характеристики как функции обобщенной расстройки показаны на рис. 4.12. Сплошной линией показаны точные, а пунктирной – приближенные значения, полученные из (4.40).
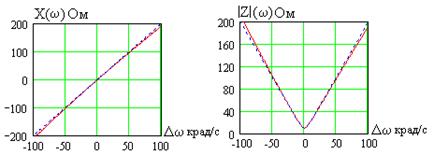
Рис. 4.12
Проведем расчет комплексного коэффициента передачи, приближенно заменив в числителе (4.31) 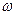 на
на 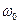 ,
,
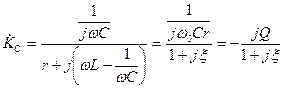 . (4.41)
. (4.41)
Частотные характеристики последовательного колебательного контура в координатах обобщенной расстройки имеют вид
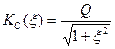 , (4.42)
, (4.42)
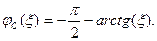 (4.43)
(4.43)
Зависимости АЧХ 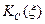 и ФЧХ
и ФЧХ 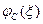 показаны на рис. 4.13 пунктирными линиями. Их точные значения показаны сплошными кривыми.
показаны на рис. 4.13 пунктирными линиями. Их точные значения показаны сплошными кривыми.
Как видно, расчеты частотных характеристик в координатах обобщенной расстройки имеют вполне удовлетворитель-
ную точность в достаточно широкой окрестности резонансной частоты, то есть там, где они и представляют практический интерес.
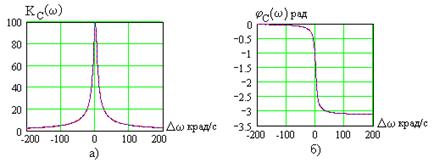
Рис. 4.13
С помощью обобщенной расстройки можно проводить расчеты токов и напряжений в контуре:
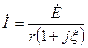 , (4.44)
, (4.44)
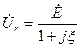 , (4.45)
, (4.45)
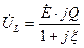 , (4.46)
, (4.46)
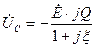 , (4.47)
, (4.47)
Выражения и вычисления существенно упрощаются.
Запишите самостоятельно выражения для амплитуд и начальных фаз тока и напряжений на элементах контура. Постройте их зависимости от частоты и обобщенной расстройки, оцените погрешность вычислений в координатах 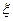 .
.
4.8. Полоса пропускания и коэффициент
прямоугольности
Определим полосу пропускания контура, расчет проведем в координатах обобщенной расстройки (рис. 4.14).
 Максмум АЧХ контура равен добротности
Максмум АЧХ контура равен добротности 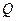 , тогда полоса пропускания определяется на уровне
, тогда полоса пропускания определяется на уровне
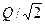 .
.
С учетом (4.42) урав-
нение имеет
вид Рис. 4.14
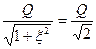 (4.48)
(4.48)
и его решения равны
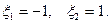
Интервал обобщенной расстройки в полосе пропускания
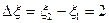 ,
,
с другой стороны из (4.38)
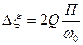 ,
,
тогда получим уравнение
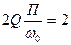 ,
,
а полоса пропускания будет равна
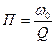 . (4.49)
. (4.49)
Как видно, полоса пропускания контура с заданной частотой настройки 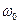 определяется только его добротностью. Высокодобротный контур позволяет реализовать узкополосный частотный фильтр. Как уже отмечалось, большие значения
определяется только его добротностью. Высокодобротный контур позволяет реализовать узкополосный частотный фильтр. Как уже отмечалось, большие значения 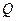 обеспечить достаточно сложно.
обеспечить достаточно сложно.

Для определения коэффициента прямоугольности 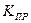 необходимо найти полосу пропускания контура
необходимо найти полосу пропускания контура 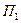 на уровне 1/10 от максимума. Для этого составим уравнение в координатах
на уровне 1/10 от максимума. Для этого составим уравнение в координатах 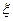 ,
,
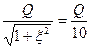 , (4.50)
, (4.50)
решения которого равны
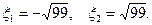
Интервал величин обобщенной расстройки в полосе пропускания на уровне 1/10 от максимума равен
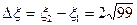 ,
,
тогда получим уравнение
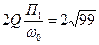 ,
,
а полоса пропускания 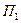 будет равна
будет равна
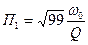 . (4.51)
. (4.51)
В результате коэффициент прямоугольности колебательного контура оказывается равным
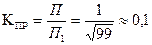 .
.
Как видно, последовательный колебательный контур является полосовым частотным фильтром с низкой избирательностью.
4.9. Влияние внутреннего сопротивления источника
сигнала и нагрузки на резонансные свойства контура
Рассмотрим контур с подключенным реальным источником напряжения 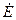 (
( 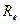 - его внутреннее сопротивление) и сопротивлением нагрузки
- его внутреннее сопротивление) и сопротивлением нагрузки 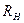 (рис. 4.15). Можно провести анализ этой цепи отдельно, однако целесообразнее преобразовать
(рис. 4.15). Можно провести анализ этой цепи отдельно, однако целесообразнее преобразовать
ее к уже рассмотренной цепи вида рис. 4.5 (с идеальным источником напряжения и без нагрузки) и воспользоваться уже полученными результатами анализа.
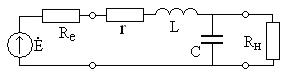
Рис. 4.15
 Как видно, сопротивление источника
Как видно, сопротивление источника 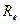 просто складывается с
просто складывается с 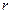 , увеличивая сопротивление потерь контура. Нагрузка же подключена параллельно емкости, и тогда параллельное соединение
, увеличивая сопротивление потерь контура. Нагрузка же подключена параллельно емкости, и тогда параллельное соединение 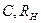 необходимо эквивалентно преобразовать в последовательное соединение элементов
необходимо эквивалентно преобразовать в последовательное соединение элементов 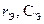 (как по-
(как по-
Рис. 4.16 казано на рис. 4.16). Эти
цепи эквивалентны, если равны их полные комплексные сопротивления, тогда получим
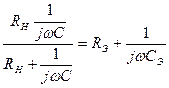 .
.
Преобразуя дроби и приводя обе части равенства к алгебраической форме записи комплексных чисел, можно записать
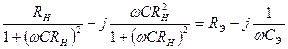 .
.
Комплексные числа равны тогда и только тогда, когда равны отдельно их действительные и мнимые части, поэтому после алгебраических преобразований получим два уравнения для неизвестных 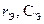 ,
,
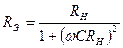 , (4.52)
, (4.52)
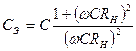 . (4.53)
. (4.53)
Проделайте необходимые преобразования самостоятельно.
Как видно, эквивалентные параметры последовательной цепи зависят от частоты и, строго говоря, такое преобразование возможно только на фиксированной частоте. При анализе колебательного контура интерес представляет окрестность его резонансной частоты 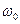 , поэтому в (4.52) и (4.53), приняв
, поэтому в (4.52) и (4.53), приняв 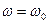 и условие
и условие
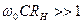 , (4.54)
, (4.54)
получим
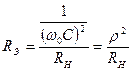 , (4.55)
, (4.55)
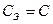 . (4.56)
. (4.56)
Эти равенства является точными на частоте 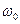 и приближенными в ее окрестности. На рис. 4.17 показаны зависимости эквивалентных сопротивления
и приближенными в ее окрестности. На рис. 4.17 показаны зависимости эквивалентных сопротивления 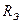 и емкости
и емкости 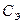 от абсолютной
от абсолютной
расстройки при 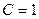 нФ и
нФ и 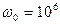 рад/с и различных значениях сопротивления нагрузки
рад/с и различных значениях сопротивления нагрузки 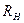 . Как видно, при больших
. Как видно, при больших 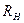 , и особенно при выполнении условия (4.54), величины
, и особенно при выполнении условия (4.54), величины 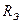 и
и 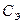 практически постоянны в широкой окрестности резонансной частоты.
практически постоянны в широкой окрестности резонансной частоты.
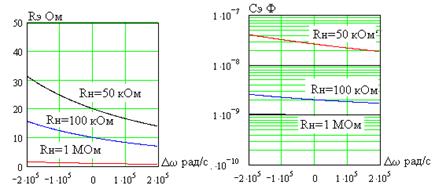
Рис. 4.17
 Таким образом эквивалентная схема последовательного колебательного контура с реальным источником сигнала и нагрузкой имеет вид, показанный на рис. 4.18, где
Таким образом эквивалентная схема последовательного колебательного контура с реальным источником сигнала и нагрузкой имеет вид, показанный на рис. 4.18, где 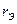 - эквивалентное сопротивление потерь, рав-
- эквивалентное сопротивление потерь, рав-
Рис. 4.18 ное
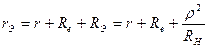 . (4.56)
. (4.56)
Контур рис. 4.18 уже изучен, его резонансные свойства определяются эквивалентной добротностью 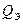 ,
,
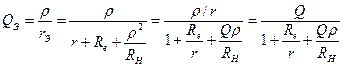 . (4.57)
. (4.57)
Как видно, внутреннее сопротивление источника сигнала 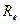 снижает эквивалентную добротность, его влияние будет мало, если
снижает эквивалентную добротность, его влияние будет мало, если
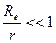 или
или 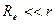 , (4.58)
, (4.58)
Собственное сопротивление потерь 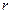 достаточно мало (доли Ома - единицы Ом), поэтому источник сигнала для последовательного колебательного контура должен быть практически идеальным.
достаточно мало (доли Ома - единицы Ом), поэтому источник сигнала для последовательного колебательного контура должен быть практически идеальным.
Нагрузка контура также снижает его добротность, чем больше 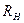 , тем меньше падает
, тем меньше падает 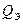 . Для того, чтобы влияние нагрузки было невелико, необходимо выполнение условия
. Для того, чтобы влияние нагрузки было невелико, необходимо выполнение условия
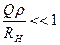 или
или 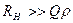 . (4.59)
. (4.59)
На практике величина характеристического сопротивления 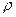 составляет сотни Ом – килоОмы, добротность лежит в пределах от нескольких десятков до 150, тогда произведение
составляет сотни Ом – килоОмы, добротность лежит в пределах от нескольких десятков до 150, тогда произведение 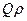 составляет десятки - сотни килоОм. С учетом сделанных оценок необходимое сопротивление нагрузки при условии (4.59) оказывается достаточно большим, например, 1 МОм, что крайне сложно обеспечить на практике.
составляет десятки - сотни килоОм. С учетом сделанных оценок необходимое сопротивление нагрузки при условии (4.59) оказывается достаточно большим, например, 1 МОм, что крайне сложно обеспечить на практике.
Для ослабления влияния нагрузки на добротность контура используют ее неполное включение, один из вариантов схемы показан на рис. 4.19.
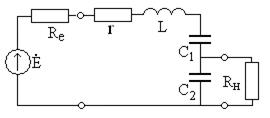
Рис. 4.19
Проведите самостоятельно анализ этой цепи аналогично предыдущей, преобразовав параллельное соединение 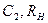 в последовательное, получите выражение для эквивалентной добротности, в результате можно записать
в последовательное, получите выражение для эквивалентной добротности, в результате можно записать
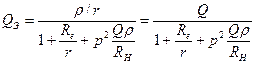 , (4.60)
, (4.60)
где 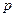 - коэффициент включения нагрузки в контур, равный
- коэффициент включения нагрузки в контур, равный
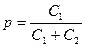 . (4.61)
. (4.61)
Требования к сопротивлению нагрузки определяются неравенством
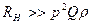 , (4.62)
, (4.62)
что значительно слабее (4.59). Например, при 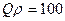 кОм и
кОм и 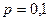 (типичное значение) необходимо выполнение условия
(типичное значение) необходимо выполнение условия 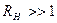 кОм, что вполне приемлемо на практике.
кОм, что вполне приемлемо на практике.
4.10. Расчеты цепей с последовательными
колебательными контурами
Расчет гармонических токов и напряжений в электрических цепях с колебательными контурами проводится методом комплексных амплитуд чаще всего в координатах обобщенной расстройки.
 Рассмотрим пример, показанный на рис. 4.20, в котором на заданной частоте
Рассмотрим пример, показанный на рис. 4.20, в котором на заданной частоте 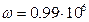 рад/с при
рад/с при 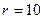 Ом,
Ом, 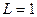 мГн,
мГн, 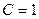 нФ,
нФ, 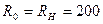 Ом и
Ом и 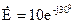 В необходимо определить комплексную амплитуду напряжения на нагрузке
В необходимо определить комплексную амплитуду напряжения на нагрузке 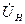 . Расчет в координатах частоты
. Расчет в координатах частоты 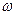 будет достаточно громоздким (проведите его самостоятельно, чтобы убедиться в этом). Рис. 4.20
будет достаточно громоздким (проведите его самостоятельно, чтобы убедиться в этом). Рис. 4.20
Резонансная частота 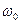
контура равна
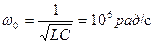 ,
,
а добротность соответственно
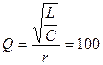 .
.
В координатах обобщенной расстройки 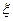 , равной
, равной
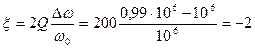 ,
,
сопротивление 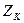 последовательного колебательного контура
последовательного колебательного контура 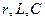 равно
равно 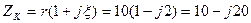 Ом.
Ом.
Сопротивление 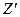 параллельного соединения контура с нагрузкой определяется выражением
параллельного соединения контура с нагрузкой определяется выражением
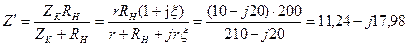 Ом.
Ом.
Вычислим общее сопротивление цепи,
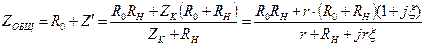 ,
,
в результате получим
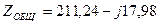 Ом.
Ом.
Комплексная амплитуда тока в цепи равна
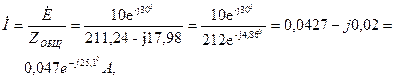
а напряжения на нагрузке соответственно
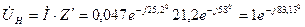 В.
В.
Переход к координатам обобщенной расстройки существенно упрощает расчеты цепей с колебательными контурами. При расчетах широко используют известные выражения для коэффициента передачи и других характеристик контура.

 Рассмотрим пример, показанный на рис.4.21 при
Рассмотрим пример, показанный на рис.4.21 при 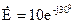 В
В 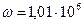 рад/с,
рад/с, 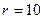 Ом,
Ом, 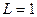 мГн и
мГн и 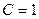 нФ. Необходимо рассчитать мгновенные значения напряжения на емкости последовательного колебательного контура
нФ. Необходимо рассчитать мгновенные значения напряжения на емкости последовательного колебательного контура 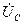 .
.
Резонансная частота 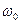 и добротность
и добротность 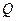 равны Рис. 4.21
равны Рис. 4.21
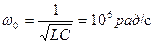 ,
, 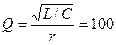 ,
,
тогда для обобщенной расстройки получим
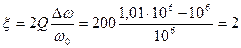 .
.
Комплексный коэффициент передачи 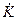 определяется выражением
определяется выражением
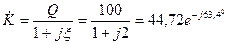 ,
,
тогда комплексная амплитуда напряжения на емкости равна
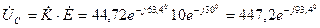 В,
В,
а для его мгновенных значений получим
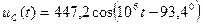 В.
В.
4.11. Моделирование последовательного колебательного
контура
На рис. 4.22 показана модель последовательного колебательного контура 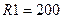 Ом,
Ом, 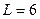 мГн и
мГн и 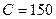 пФ с нагрузкой
пФ с нагрузкой 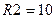 МОм в пакете программ MicroCAP7. На рис. 4.23 приведены результаты моделирования в АЧХ и ФЧХ режиме «Stepping» при изменении сопротивления потерь
МОм в пакете программ MicroCAP7. На рис. 4.23 приведены результаты моделирования в АЧХ и ФЧХ режиме «Stepping» при изменении сопротивления потерь 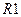 от 50 Ом (верхние кривые) до 150 Ом (нижние
от 50 Ом (верхние кривые) до 150 Ом (нижние
кривые) с шагом 50 Ом.
Рис.4.22 На рис. 4.24 пока-
заны аналогичные зависимости при 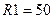 Ом и изменении сопротивления нагрузки от
Ом и изменении сопротивления нагрузки от 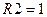 МОм (нижние кривые) до
МОм (нижние кривые) до 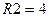 МОм верхние кривые) с шагом 1МОм .
МОм верхние кривые) с шагом 1МОм .
Как видно по результатам моделирования, максимум АЧХ снижается с ростом сопротивления потерь и уменьшением сопротивления нагрузки, причем даже при большом 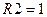 МОм добротность контура существенно уменьшается. При этих условиях АЧХ и ФЧХ становятся более пологими.
МОм добротность контура существенно уменьшается. При этих условиях АЧХ и ФЧХ становятся более пологими.
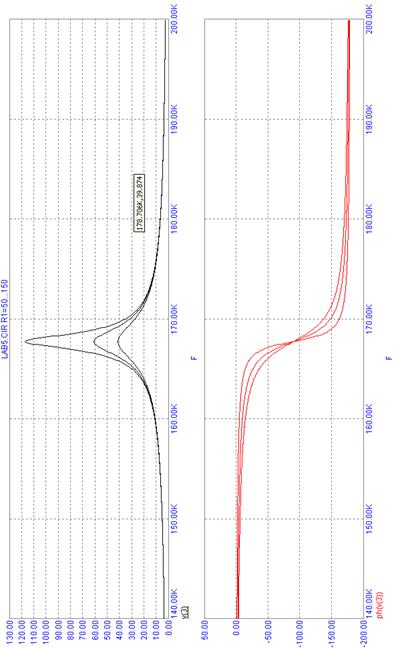
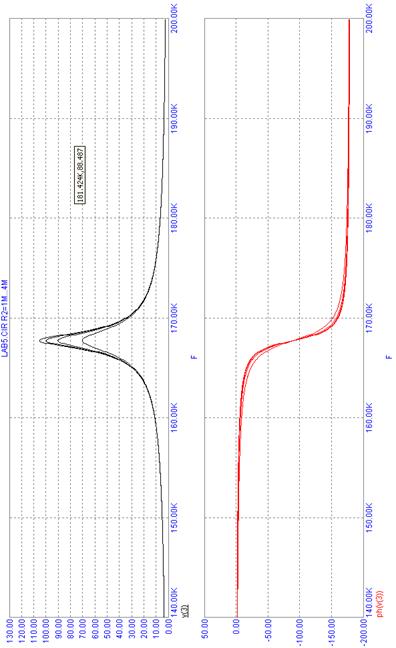
На рис. 4.25 представлены результаты моделирования контура при изменении его емкости от 100пФ (правая кривая) до 200пФ (левая кривая) с шагом 50 пФ для 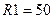 Ом. Такие изменения происходят при настройке колебательного контура в радиоприемнике с помощью конденсатора переменной емкости.
Ом. Такие изменения происходят при настройке колебательного контура в радиоприемнике с помощью конденсатора переменной емкости.
Проведите расчеты, подтверждающие результаты моделирования, например, вычислите максимальные значения АЧХ при соответствующих параметрах цепи.
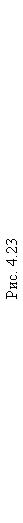

4.12. Применение последовательного колебательного
контура
Последовательный колебательный контур широко используется как узкополосный частотный фильтр. Таким фильтром является преселектор (предварительный селектор), который присутствует в любом супергетеродинном радиоприемнике (факультативно поинтересуйтесь у преподавателя, как работает супергетеродинный радиоприемник), его условная схема показана на рис. 4.26. Антенна приемника включена в контур как источник сигнала, а напряжение с емкости 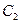 подается на вход усилителя высокочастотного сигнала (УВЧ), входное сопротивление которого является нагрузкой колебательного контура. Так как транзисторный УВЧ имеет невысо-
подается на вход усилителя высокочастотного сигнала (УВЧ), входное сопротивление которого является нагрузкой колебательного контура. Так как транзисторный УВЧ имеет невысо-
Рис. 4.26 кое входное сопротивление,
то используется неполное включение нагрузки. Задача преселектора – фильтрация «зеркального канала» приема в супергетеродинном приемнике.
 На базе последовательного колебательного контура можно реализовать режекторный фильтр, пример которого показан на рис. 4.27. На рис 4.28 показана его модель при
На базе последовательного колебательного контура можно реализовать режекторный фильтр, пример которого показан на рис. 4.27. На рис 4.28 показана его модель при 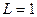 мГн,
мГн, 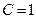 нФ и
нФ и 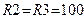 Ом, сопротив-
Ом, сопротив-
лении потерь катушки ин-
дуктивности 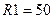 Ом и сопротивлении нагрузки
Ом и сопротивлении нагрузки
Рис. 4.27 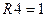 кОм, а на рис. 4.29 –
кОм, а на рис. 4.29 –
АЧХ и ФЧХ.
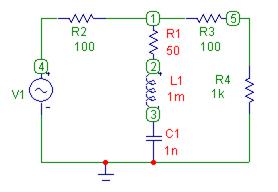
Рис. 4.28
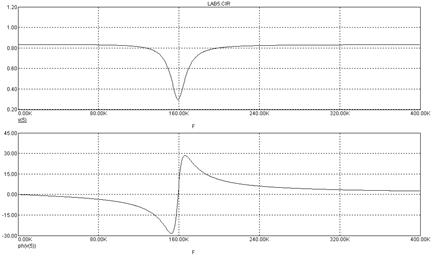
Рис. 4.29
Как видно, фильтр подавляет сигнал в окрестности частоты 160 кГц. Нетрудно спроектировать такой фильтр на частоту 50 или 100 Гц, что часто необходимо в биомедицинской аппаратуре, питающейся от силовой сети переменного тока 220В с частотой 50 Гц (проведите необходимые расчеты и схемотехническое моделирование).
4.13. Задания для самостоятельного решения
Задание 4.1. Определите сопротивление потерь колебательного контура при 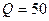 ,
, 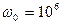 рад/с и
рад/с и 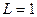 мГн.
мГн.
Задание 4.2. Определите сопротивление потерь колебательного контура при полосе пропускания 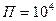 рад/с и
рад/с и 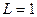 мГн.
мГн.
Задание 4.4. Определите полосу пропускания колебательного контура при 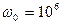 рад/с,
рад/с, 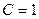 нФ и сопротивлении потерь
нФ и сопротивлении потерь 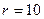 Ом.
Ом.
Задание 4.4. Определите добротность 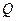 колебательного контура при
колебательного контура при 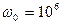 рад/с и полосе пропускания
рад/с и полосе пропускания 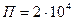 рад/с.
рад/с.
Задание 4.5. Определите напряжение на катушке индуктивности контура рис. 4.30 при 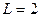 мГн,
мГн, 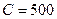 пФ,
пФ,

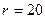 Ом,
Ом, 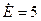 В,
В, 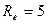 Ом и
Ом и 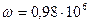 рад/с. Расчет проведите обычным методом комплексных амплитуд и используя теорию колебательных контуров в координатах обобщенной расстройки, сравните результаты.
рад/с. Расчет проведите обычным методом комплексных амплитуд и используя теорию колебательных контуров в координатах обобщенной расстройки, сравните результаты.
Рис. 4.30
Задание 4.6. Определите напряжение на емкости контура рис. 4.31 при 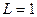 мГн,
мГн, 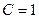 нФ,
нФ, 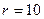 Ом,
Ом, 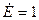 В,
В, 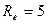 Ом и
Ом и 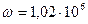 рад/с. Расчет проведите обычным
рад/с. Расчет проведите обычным
 методом комплексных амплитуд и используя теорию колебательных контуров в координатах обобщенной расстройки
методом комплексных амплитуд и используя теорию колебательных контуров в координатах обобщенной расстройки
сравните результаты. Рис. 4.31
Задание 4.7. Вычислите резонансные значения тока и напряжение на емкости контура при 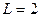 мГн,
мГн, 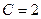 нФ,
нФ, 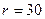 Ом и ЭДС идеального источника напряжения
Ом и ЭДС идеального источника напряжения 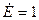 В.
В.
 Задание 4.8. В координатах обобщенной расстройки вычислите напряжение
Задание 4.8. В координатах обобщенной расстройки вычислите напряжение 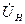 на нагрузке в цепи на рис. 4.32 при
на нагрузке в цепи на рис. 4.32 при 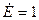 В,
В, 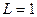 мГн,
мГн, 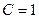 нФ,
нФ, 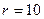 Ом, Рис. 4.32
Ом, Рис. 4.32
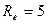 Ом,
Ом, 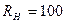 кОм и
кОм и 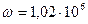 рад/с.
рад/с.
 Задание 4.9. Получите выражение для АЧХ цепи, показанной на рис. 4.33, постройте ее график. Проанализируйте влияние нагрузки
Задание 4.9. Получите выражение для АЧХ цепи, показанной на рис. 4.33, постройте ее график. Проанализируйте влияние нагрузки 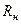 и сопротивлений
и сопротивлений 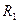 и
и 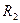 на форму АЧХ.
на форму АЧХ.
Рис. 4.33
Дата добавления: 2015-06-17; просмотров: 14006;
