Фазочастотная характеристика (ФЧХ) – это зависимость от частоты аргумента комплексного коэффициента передачи. Она представляет собой сдвиг фаз между выходным и входным сигналами.
Обычно выражение для 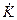 представляет собой дробь с комплексными числителем и знаменателем, которую необходимо представить в виде
представляет собой дробь с комплексными числителем и знаменателем, которую необходимо представить в виде
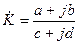 . (1.18)
. (1.18)
Тогда модуль частного (дроби) равен частному модулей числителя и знаменателя,
 , (1.19)
, (1.19)
а ее аргумент – разности аргументов числителя и знаменателя,
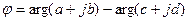 . (1.20)
. (1.20)
Аргумент комплексного числа 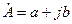 определяется выражением
определяется выражением
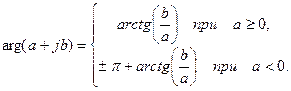 (1.21)
(1.21)
Численные значения АЧХ безразмерны, а ФЧХ измеряется в угловых единицах (радианах или градусах).
В инженерной практике широко используется измерение АЧХ в децибелах (дБ). Если рассматриваются модули коэффициентов 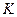 передачи напряжения или тока, то их значение в децибелах равно
передачи напряжения или тока, то их значение в децибелах равно
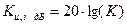 . (1.22)
. (1.22)
Если же речь идет о коэффициенте передачи мощности 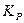 , то
, то
 . (1.23)
. (1.23)
Логарифмическая мера АЧХ весьма удобна при анализе четырехполюсников. Если  , то получим, что
, то получим, что 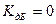 дБ и амплитуда сигнала не меняется при прохождении через четырехполюсник. Если
дБ и амплитуда сигнала не меняется при прохождении через четырехполюсник. Если 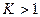 , то
, то 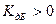 и происходит усиление сигнала, а если наоборот, то
и происходит усиление сигнала, а если наоборот, то 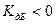 и наблюдается ослабление (затухание) сигнала. Основным достоинством логарифмической меры является возможность отображать графически широкий диапазон изменения АЧХ от маленьких величин
и наблюдается ослабление (затухание) сигнала. Основным достоинством логарифмической меры является возможность отображать графически широкий диапазон изменения АЧХ от маленьких величин 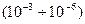 или
или 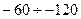 дБ до больших значений
дБ до больших значений 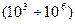 или
или 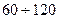 дБ.
дБ.
Измерение коэффициентов передачи в децибелах удобно при их перемножении, например, при каскадном соединении согласованно нагруженных четырехполюсников (эти вопросы рассматриваются в дальнейшем), при этом значения в децибелах будут складываться.
Определим АЧХ и ФЧХ цепи, показанной на рис. 1.12. Для найденного комплексного коэффициента передачи по напряжению модуль (АЧХ) и аргумент (ФЧХ) соответственно равны
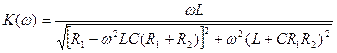 ,
,
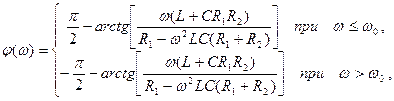
где
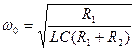 .
.
На рис. 1.21 показан график АЧХ четырехполюсника, показанного на рис. 1.18 при 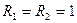 кОм,
кОм, 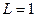 мГн и
мГн и 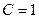 нФ. Максимум АЧХ имеет место на частоте
нФ. Максимум АЧХ имеет место на частоте 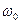 , в чем нетрудно убедиться, взяв производную
, в чем нетрудно убедиться, взяв производную 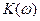 и приравняв ее нулю. На рис. 1.22 приведен график ФЧХ четырехполюсника.
и приравняв ее нулю. На рис. 1.22 приведен график ФЧХ четырехполюсника.
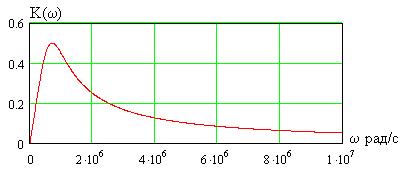
Рис. 1.21
На частотах 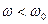 ФЧХ
ФЧХ  , то есть выходное
, то есть выходное
напряжение опережает по фазе входное, а если 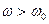 , то наоборот. На частоте
, то наоборот. На частоте 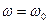 сдвиг фаз между этими напряжениями равен нулю (они синфазны).
сдвиг фаз между этими напряжениями равен нулю (они синфазны).
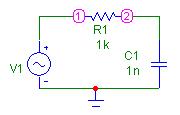
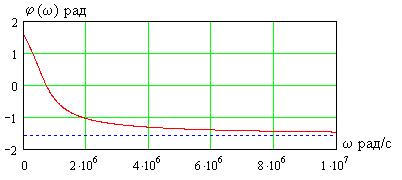
Рис. 1.22
На рис. 1.23а показана та же АЧХ, что и на рис. 1.15, но в децибелах, а на рис. 1.23б – еще и в логарифмическом масштабе по оси частот. Как видно, переход к логарифмическим масштабам по оси ординат (дБ) и оси частот позволяет разборчиво представить АЧХ в широком диапазоне значений. Недостатком подобных графиков является искажение формы кривых по сравнению с равномерным масштабом на рис. 1.21.
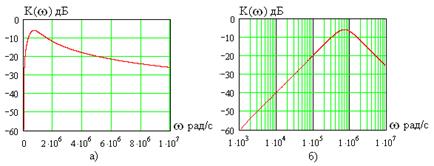
Рис. 1.23
1.5. Схемотехническое моделирование
Рассмотрим применение пакета программ схемотехнического моделирования MicroCAP7 для анализа частотных характеристик четырехполюсников.
Пример моделируемой цепи показан на рис. 1.24. Проведите расчет ее частотных характеристик при 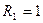 кОм и
кОм и 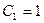 нФ.
нФ.
На рис. 1.25 представлены
зависимости от частоты модуля и аргумента входного сопротив-
Рис. 1.24 ления, модуль сопротивления за-
дается выражением 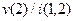 , а аргумент – функцией
, а аргумент – функцией 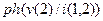 . Вычислите значения этих характеристик на частоте 200кГц и сравните с результатами моделирования.
. Вычислите значения этих характеристик на частоте 200кГц и сравните с результатами моделирования.
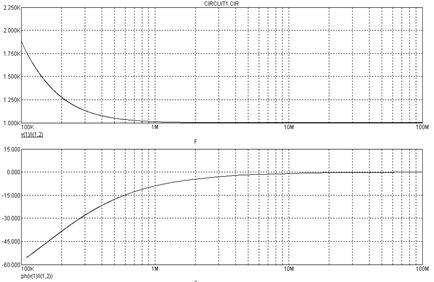
Рис. 1.25
На рис. 1.26 показаны зависимости от частоты модуля (АЧХ) и аргумента (ФЧХ) комплексного коэффициента передачи цепи рис. 1.24.
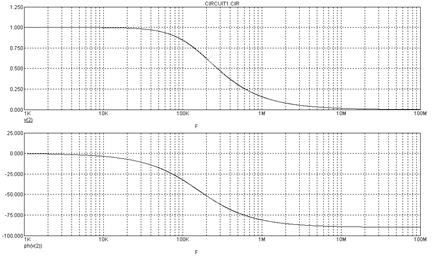
Рис. 1.26
Схемотехническое моделирование в режиме «AC Analysis» позволяет получить различные частотные характеристики исследуемой цепи.
Рассмотрим модель той же цепи, но с подключенной нагрузкой  кОм (рис. 1.27). На рис. 1.28 показаны результаты моделирования АЧХ (в децибелах) и ФЧХ в режиме «Stepping» при изменении
кОм (рис. 1.27). На рис. 1.28 показаны результаты моделирования АЧХ (в децибелах) и ФЧХ в режиме «Stepping» при изменении 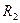 от 1 кОм (верхняя кривая) до 200 Ом (нижняя кривая) с одинаковым шагом 200 Ом.
от 1 кОм (верхняя кривая) до 200 Ом (нижняя кривая) с одинаковым шагом 200 Ом.
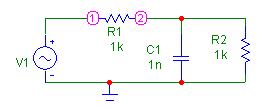
Рис. 1.27
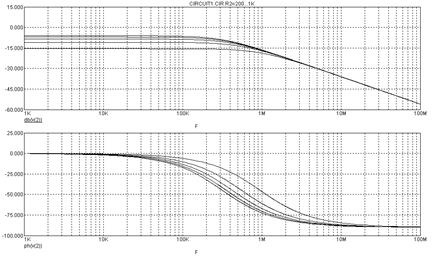
Рис. 1.28
Как видно, моделирование позволяет исследовать влияние параметра цепи на частотные характеристики с целью, например, выбора его оптимального значения.
1.6. Задания для самостоятельного решения
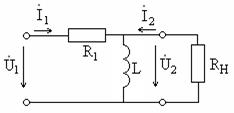 Задание 1.1. Определите входное сопротивление четырехполюсника, показанного на рис. 1.29. Получите формулы для его модуля и аргумента, активной и реактивной составляющих. С помощью пакета программ MathCAD постройте графики для
Задание 1.1. Определите входное сопротивление четырехполюсника, показанного на рис. 1.29. Получите формулы для его модуля и аргумента, активной и реактивной составляющих. С помощью пакета программ MathCAD постройте графики для 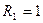 кОм и
кОм и 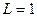 мГн при отсутствии нагрузки (
мГн при отсутствии нагрузки (  ) и при ее наличии (
) и при ее наличии ( 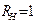 кОм).
кОм).
Рис. 1.29
Задание 1.2. Для цепи рис. 1.30 при 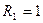 кОм,
кОм,
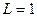 мГн и
мГн и 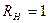 кОм на частоте
кОм на частоте 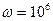 рад/с определите, при каком комплексном сопротивлении
рад/с определите, при каком комплексном сопротивлении  реального источника сигнала в нагруженный четырехполюсник будет передана максимальная мощность. Вычислите величину этой мощности при ЭДС источника напряжения
реального источника сигнала в нагруженный четырехполюсник будет передана максимальная мощность. Вычислите величину этой мощности при ЭДС источника напряжения 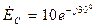 В.
В.
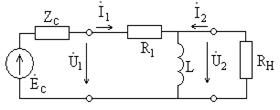
Рис. 1.30
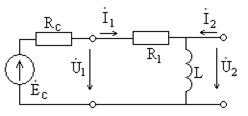
Задание 1.3. Для четырехполюсника с подключенным источником напряжения с ЭДС 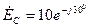 В и
В и 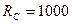 Ом, показанного на рис. 1.31, определите выходное сопротивление, используя теорему об эквивалентном источнике. Получите формулы для его модуля и аргумента, активной и реактивной составляющих. С помощью пакета программ MathCAD постройте соответствующие графики для
Ом, показанного на рис. 1.31, определите выходное сопротивление, используя теорему об эквивалентном источнике. Получите формулы для его модуля и аргумента, активной и реактивной составляющих. С помощью пакета программ MathCAD постройте соответствующие графики для 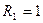 кОм и
кОм и 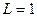 мГн.
мГн.
 На частоте
На частоте 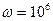 рад/с определите, при каком комплексном сопротивлении нагрузки
рад/с определите, при каком комплексном сопротивлении нагрузки 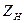 , подключенной к четырехполюснику рис. 1.31, в нее будет передана максимальная мощность.
, подключенной к четырехполюснику рис. 1.31, в нее будет передана максимальная мощность.
Рис. 1.31
Задание 1.4. Рассчитайте входную и выходную проводимости показанного на рис. 1.32 четырехполюсника, рассмотрите ее в диапазоне частот при 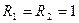 кОм,
кОм, 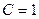 нФ,
нФ, 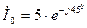 мА,
мА, 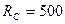 Ом и
Ом и 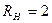 кОм. Постройте соответствующие графики.
кОм. Постройте соответствующие графики.
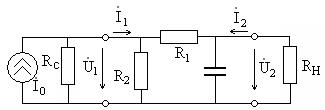
Рис. 1.32
Задание 1.5. Рассчитайте комплексный коэффициент передачи и постройте годографы КЧХ четырехполюсников, схемы которых показаны на рис. 1.33. Определите их АЧХ и ФЧХ, постройте их графики.
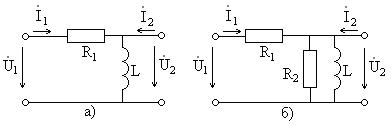
Рис. 1.33
Задание 1.6. Выполните задания 1.1-1.5 методом схемотехнического моделирования. Сравните полученные результаты с расчетными. Сравните АЧХ в линейном масштабе и в децибелах, оцените их преимущества и недостатки.
Дата добавления: 2015-06-17; просмотров: 7179;
