Теоретическая часть. Всякое тело можно мысленно разбить на столь большое число малых частей (материальных точек) так, что размеры их будут малы по сравнению с размерами всего
Всякое тело можно мысленно разбить на столь большое число  малых частей (материальных точек) так, что размеры их будут малы по сравнению с размерами всего тела. Следовательно, тело всегда можно рассматривать как систему из
малых частей (материальных точек) так, что размеры их будут малы по сравнению с размерами всего тела. Следовательно, тело всегда можно рассматривать как систему из  материальных точек, причем масса тела
материальных точек, причем масса тела 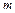 равна сумме масс всех этих точек:
равна сумме масс всех этих точек: 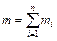 , где
, где 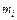 – масса i-той материальной точки.
– масса i-той материальной точки.
Рассмотрим движение твердого тела, закрепленного в одной неподвижной точке О, вокруг которой тело может свободно вращаться. Точка О называется центром вращения твердого тела. Совместим с этой точкой начало неподвижной системы координат. Тогда положение в пространстве i-той точки тела полностью определяется радиус-век-тором 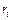 , проведенным из точки О в эту точку.
, проведенным из точки О в эту точку.
Сумма произведений масс всех материальных точек тела на квадраты их расстояний до оси вращения называется моментом инерции тела относительно этой оси. Момент инерции тела относительно оси О равен:
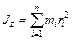 , (10.1)
, (10.1)
где 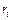 – расстояние от i-той материальной точки до оси вращения. При вычислении момента инерции, тело разбивают на бесконечно большое число бесконечно малых элементов с массами
– расстояние от i-той материальной точки до оси вращения. При вычислении момента инерции, тело разбивают на бесконечно большое число бесконечно малых элементов с массами 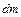 . Поэтому в формуле (10.1) сумму
. Поэтому в формуле (10.1) сумму 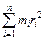 заменяют интегралом по объему этого тела:
заменяют интегралом по объему этого тела:
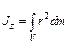 , (10.2)
, (10.2)
 где
где 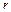 – расстояние от элемента
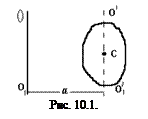
– расстояние от элемента 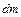 до оси Оz. По мере удаления тела от оси вращения, проходящей через центр инерции (центр масс), возрастает момент инерции тела. Это доказывает теорема Штейнера: момент инерции Jz' тела относительно любой оси ОО1 равен сумме момента инерции Jz тела относительно оси О'O1', проведенной через центр инерции С тела параллельно ОО1, и произведения массы
до оси Оz. По мере удаления тела от оси вращения, проходящей через центр инерции (центр масс), возрастает момент инерции тела. Это доказывает теорема Штейнера: момент инерции Jz' тела относительно любой оси ОО1 равен сумме момента инерции Jz тела относительно оси О'O1', проведенной через центр инерции С тела параллельно ОО1, и произведения массы 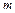 тела на квадрат расстояния а между этими осями (рис. 10.1):
тела на квадрат расстояния а между этими осями (рис. 10.1):
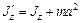 , (10.3)
, (10.3)
В таблице 10.1 приведены формулы для вычисления моментов инерции однородных тел простейшей формы.
Таблица 10.1
| Тело | Положение оси Оz | Момент инерции |
Полый тонкостенный цилиндр радиуса R, имеющий массу 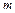
| Ось симметрии | 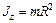
|
| Сплошной цилиндр (или диск) радиуса R, имеющий массу m | Ось симметрии | 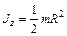
|
Прямой тонкий стержень, имеющий длину 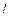 и массу и массу 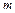
| Ось перпендикулярна к стержню и проходит через его середину | 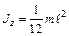
|
| Тот же стержень | Ось перпендикулярна к стержню и проходит через его конец | 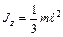
|
Шар радиуса R, имеющий массу 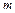
| Ось проходит через центр шара | 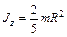
|
| Тот же шар | Ось проходит на расстоянии а от центра шара | 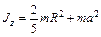
|
Вычислить момент инерции тела относительно оси можно используя момент инерции его относительно точки. Сам по себе момент инерции тела относительно точки не играет никакой роли в динамике. Он является чисто вспомогательным понятием, служащим для упрощения вычислений. Моментом инерции тела относительно точки О называется сумма произведений масс материальных точек, из которых тело состоит, на квадраты их расстояний R до точки О. В случае непрерывного распределения масс эта сумма сводится к интегралу 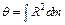 . Но момент инерции
. Но момент инерции 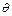 не следует смешивать с моментом инерции
не следует смешивать с моментом инерции 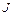 относительно оси. В случае момента
относительно оси. В случае момента 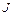 массы
массы 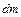 умножаются на квадраты расстояний до этой оси, а в случае момента
умножаются на квадраты расстояний до этой оси, а в случае момента 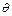 – до неподвижной точки.
– до неподвижной точки.
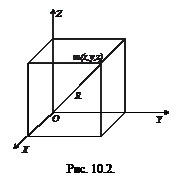
Рассмотрим сначала одну материальную точку с массой 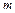 и с координатами х, y, z относительно прямоугольной системы координат (рис.10.2). Квадраты расстояний ее до координатных осей X, Y, Z равны соответственно
и с координатами х, y, z относительно прямоугольной системы координат (рис.10.2). Квадраты расстояний ее до координатных осей X, Y, Z равны соответственно 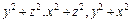 , а моменты инерции относительно тех же осей:
, а моменты инерции относительно тех же осей: 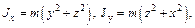
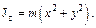 Сложив эти три равенства, получим:
Сложив эти три равенства, получим: 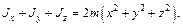 Но
Но 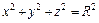 , где R –- расстояние точки
, где R –- расстояние точки 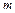 от начала координат О. Поэтому:
от начала координат О. Поэтому:
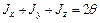 , (10.4)
, (10.4)
где 
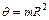 .
.
 Это соотношение справедливо не только для одной материальной точки, но и для произвольного тела, так как тело можно рассматривать как совокупность материальных точек. Таким образом, сумма моментов инерции тела относительно трех взаимно перпендикулярных осей, пересекающихся в одной точке О, равна удвоенному моменту инерции того же тела относительно этой точки.
Это соотношение справедливо не только для одной материальной точки, но и для произвольного тела, так как тело можно рассматривать как совокупность материальных точек. Таким образом, сумма моментов инерции тела относительно трех взаимно перпендикулярных осей, пересекающихся в одной точке О, равна удвоенному моменту инерции того же тела относительно этой точки.
Если повернуть координатные оси Х, Y, Z относительно тела, оставляя углы между ними прямыми, то моменты инерции Jx, Jy, Jzизменятся. Однако их сумма останется той же самой, так как равна 2q, а величина q не зависит от ориентации координатных осей. Таким образом, сумма моментов инерции Jx, Jy, Jz относительно любых трех взаимно перпендикулярных осей, проходящих через одну точку, зависит только от положения этой точки и не меняется с изменением ориентации осей.
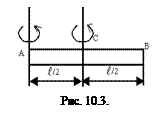 Используя соотношение (10.4), рассмотрим случай плоского распределения массы. Допустим, имеется пластинка произвольной формы с произвольным распределением вещества по ее объему. Если пластинка очень тонкая, то можно считать, что вещество распределено бесконечно тонким слоем по плоскости. Примем эту плоскость за координатную плоскость XY. Тогда z – координаты всех материальных точек будут равны нулю, а потому момент инерции q пластинки относительно начала координат О –
Используя соотношение (10.4), рассмотрим случай плоского распределения массы. Допустим, имеется пластинка произвольной формы с произвольным распределением вещества по ее объему. Если пластинка очень тонкая, то можно считать, что вещество распределено бесконечно тонким слоем по плоскости. Примем эту плоскость за координатную плоскость XY. Тогда z – координаты всех материальных точек будут равны нулю, а потому момент инерции q пластинки относительно начала координат О – 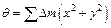 , т.е. будет равен моменту инерции пластинки относительно оси Z. Таким образом, в случае плоского распределения масс
, т.е. будет равен моменту инерции пластинки относительно оси Z. Таким образом, в случае плоского распределения масс 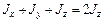 , т. е.:
, т. е.:
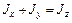 . (10.5)
. (10.5)
Приведем пример вычисления момента инерции тонкого однородного стержня относительно перпендикулярной оси.
 Пусть ось проходит через конец стержня А (рис.10.3). Для момента инерции можно написать
Пусть ось проходит через конец стержня А (рис.10.3). Для момента инерции можно написать 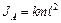 , где
, где 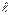 – длина стержня. Центр стержня С является его центром масс. По теореме Гюгенса-Штейнера
– длина стержня. Центр стержня С является его центром масс. По теореме Гюгенса-Штейнера 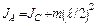 . Величину JC можно представить как сумму моментов инерции двух стержней СА и СВ, длина каждого из которых равна
. Величину JC можно представить как сумму моментов инерции двух стержней СА и СВ, длина каждого из которых равна 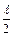 , масса
, масса 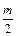 , а следовательно, момент инерции равен
, а следовательно, момент инерции равен 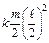 . Таким образом,
. Таким образом, 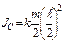 . Подставляя эти выражения в предыдущую формулу, получим:
. Подставляя эти выражения в предыдущую формулу, получим: 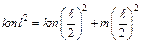 , откуда
, откуда 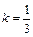 . В результате находим:
. В результате находим:
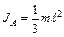 , (10.6)
, (10.6)
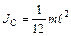 . (10.7)
. (10.7)
Аналогично можно вычислить момент инерции однородной прямоугольной пластинки и прямоугольного параллелепипеда. Пусть координатные оси X и Y проходят через центр пластинки С и параллельны ее сторонам (рис.10.4). Допустим, что все вещество пластинки смещено параллельно от оси Х к оси Y. При таком смещении все расстояния материальных точек до оси Х не изменятся. Не изменится и момент инерции Jх относительно оси Х. Но в результате смещения пластинка перейдет в бесконечно тонкий стержень длины 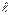 , к которому применима формула (10.7). В результате получим:
, к которому применима формула (10.7). В результате получим:
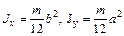 . (10.8)
. (10.8)
Момент инерции IZ пластинки относительно оси Z, перпендикулярной к ее плоскости, найдется по формуле (10.5), которая дает:
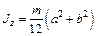 . (10.9)
. (10.9)
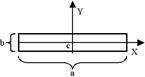 Рис.10.4
Рис.10.4
|
Формула (10.9) годится также для вычисления моментов инерции прямоугольного параллелепипеда (куба) относительно его геометрических осей. В этом можно легко убедиться, если мысленно сжать параллелепипед (куб) вдоль одной из геометрических осей в прямоугольную пластинку – при таком сжатии момент инерции относительно этой оси не изменяется. Формула (10.9) дает момент инерции прямоугольного параллелепипеда относительно той его геометрической оси, которая проходит через центр основания с длинами сторон а и b. На рис.10.4 эта ось перпендикулярна к плоскости рисунка. Для куба (а= b) формула (10.9) запишется в виде:
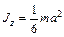 . (10.10)
. (10.10)
Наиболее простым методом является определение момента инерции тела при помощи крутильного маятника. Крутильный маятник представляет собой симметричное тело (рамка, диск и т.д.), подвешенное на тонкой нити. Если повернуть его в горизонтальной плоскости на угол a, то в закручивающейся нити подвеса возникнут силы, возвращающие тело в начальное положение. При небольших углах закручивания момент этих сил пропорционален углу (упругая деформация) 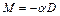 ,иуравнение движения имеет вид:
,иуравнение движения имеет вид:
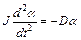 , (10.11)
, (10.11)
где J – момент инерции тела, D – постоянная момента упругих сил (постоянная кручения), a – угол закручивания (угловое перемещение). Так как уравнение (10.11) по форме не отличается от уравнения движения гармонического осциллятора: 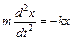 , то будут совпадать и решения обоих уравнений. Следовательно, крутильный маятник совершает гармонические колебания с частотой:
, то будут совпадать и решения обоих уравнений. Следовательно, крутильный маятник совершает гармонические колебания с частотой: 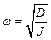 , и периодом:
, и периодом:
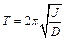 . (10.12)
. (10.12)
Для определения момента инерции тела методом крутильных колебаний надо это тело закрепить на крутильном маятнике и измерить период колебаний Т. Но при этом должны быть известны постоянная кручения и момент инерции свободной рамки. Вычислить постоянную кручения D можно следующим образом: 1) подобрать некоторое тело правильной геометрической формы (например, куб); 2) вычислить его момент инерции JЭ по формуле (10.10); 3) закрепить это тело в рамке крутильного маятника; 4) измерить период колебаний этого тела ТЭ.
Момент инерции маятника равен сумме момента инерции J0 свободной рамки и момента инерции JЭ эталонного тела (куба): 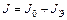 . Поэтому период колебаний маятника (рамки с закрепленным в ней кубом):
. Поэтому период колебаний маятника (рамки с закрепленным в ней кубом):
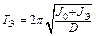 . (10.13)
. (10.13)
Отсюда находим выражение для постоянной момента упругих сил (постоянной кручения):
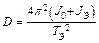 . (10.14)
. (10.14)
Если колеблется свободная рамка без тела, то ее период колебаний равен:
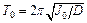 . (10.15)
. (10.15)
Момент инерции свободной рамки можно выразить из формул (10.13) и (10.15), получим:
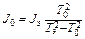 . (10.16)
. (10.16)
Дата добавления: 2015-06-17; просмотров: 1157;
