Теоретическая часть. В соответствии с основным положением классической механики, любое движения твердого тела может быть представлено как наложение двух простых видов движения:
В соответствии с основным положением классической механики, любое движения твердого тела может быть представлено как наложение двух простых видов движения: поступательного и вращательного. При поступательном движении все точки тела получают за одинаковые промежутки времени равные по величине и направлению перемещения, вследствие чего скорости и ускорения всех точек в каждый момент времени оказываются одинаковыми. При вращательном движении все точки твердого тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Для вращательного движения нужно задать положение в пространстве оси вращения и угловую скорость тела в каждый момент времени.
Представляет интерес сопоставление основных величин и формул механики вращающегося твердого тела и поступательного движения материальной точки. Для удобства такое сопоставление приведено в таблице 6.1. Из таблицы видно, что переход в соотношениях от поступательного движения к вращательному осуществляется заменой скорости – на угловую скорость, ускорения – на угловое ускорение и т. д.
Таблица 6.1
| Поступательное движение | Вращательное движение |
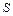 – путь – путь
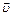 – линейная скорость – линейная скорость
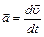 – линейное ускорение – линейное ускорение
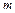 – масса тела – масса тела
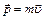 – импульс тела – импульс тела
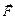 – сила – сила
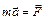 – основной закон динамики – основной закон динамики
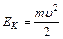 – кинетическая энергия – кинетическая энергия
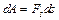 – работа – работа
| 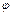 – угол поворота – угол поворота
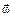 – угловая скорость – угловая скорость
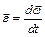 – угловое ускорение – угловое ускорение
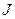 – момент инерции – момент инерции
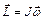 – момент импульса – момент импульса
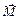 – момент силы – момент силы
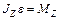 – основной закон динамики – основной закон динамики
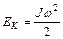 – кинетическая энергия – кинетическая энергия
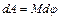 – работа – работа
|
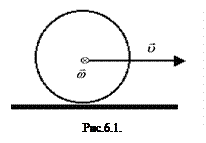 В данной работе рассматривается плоское движение, т.е. такое, при котором тело одновременно участвует в поступательном и вращательном движениях. Примером плоского движения может служить качение цилиндра по плоскости (рис. 6.1). Это движение можно представить как сумму двух движений – поступательного со скоростью
В данной работе рассматривается плоское движение, т.е. такое, при котором тело одновременно участвует в поступательном и вращательном движениях. Примером плоского движения может служить качение цилиндра по плоскости (рис. 6.1). Это движение можно представить как сумму двух движений – поступательного со скоростью 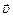 и вращательного с угловой скоростью
и вращательного с угловой скоростью 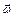 , на рисунке ось вращения проходит перпендикулярно плоскости чертежа. Таким образом, ускорение каждой точки тела складывается из ускорения поступательного движения и ускорения при вращении вокруг оси, проходящей через центр масс. Ускорение поступательного движения
, на рисунке ось вращения проходит перпендикулярно плоскости чертежа. Таким образом, ускорение каждой точки тела складывается из ускорения поступательного движения и ускорения при вращении вокруг оси, проходящей через центр масс. Ускорение поступательного движения 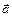 одинаково для всех точек тела и равно:
одинаково для всех точек тела и равно:
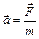 , (6.1)
, (6.1)
где 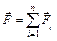 – результирующая всех внешних сил,
– результирующая всех внешних сил, 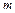 – масса тела. Направление ускорения совпадает с направлением результирующей силы
– масса тела. Направление ускорения совпадает с направлением результирующей силы 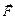 .
.
Ускорение вращательного движения 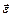 вокруг оси, проходящей через центр масс тела, равно:
вокруг оси, проходящей через центр масс тела, равно:
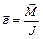 , ( 6.2)
, ( 6.2)
 где
где 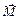 – момент всех внешних сил относительно оси, проходящей через центр масс тела,
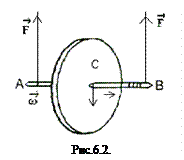
– момент всех внешних сил относительно оси, проходящей через центр масс тела, 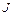 – момент инерции тела относительно той же оси. В данной работе плоское движение тела изучается на примере движения маятника Максвелла. Маятник Максвелла состоит из металлического стержня – оси AB с симметрично закрепленным на нем диском С (рис. 6.2). К концам оси прикреплены две нити, предварительно намотанные на ось. Противоположные концы нитей закреплены на верхнем кронштейне. Диск опускается под действием силы тяжести на нитях, которые разматываются до полной длины. Диск, продолжая вращательное движение в том же направлении, наматывает нити на ось, вследствие чего он поднимается вверх, замедляя при этом свое вращение. Дойдя до верхней точки, диск опять будет опускаться вниз и т. д. Диск будет совершать колебания вверх и вниз, поэтому такое устройство и называют маятником. Суть работы заключается в определении момента инерции маятника и сравнении полученных результатов с теоретически рассчитанными по известным формулам.
– момент инерции тела относительно той же оси. В данной работе плоское движение тела изучается на примере движения маятника Максвелла. Маятник Максвелла состоит из металлического стержня – оси AB с симметрично закрепленным на нем диском С (рис. 6.2). К концам оси прикреплены две нити, предварительно намотанные на ось. Противоположные концы нитей закреплены на верхнем кронштейне. Диск опускается под действием силы тяжести на нитях, которые разматываются до полной длины. Диск, продолжая вращательное движение в том же направлении, наматывает нити на ось, вследствие чего он поднимается вверх, замедляя при этом свое вращение. Дойдя до верхней точки, диск опять будет опускаться вниз и т. д. Диск будет совершать колебания вверх и вниз, поэтому такое устройство и называют маятником. Суть работы заключается в определении момента инерции маятника и сравнении полученных результатов с теоретически рассчитанными по известным формулам.
Составим уравнение поступательного движения маятника без учета силы сопротивления воздуха (рис. 6.2):
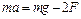 , (6.3)
, (6.3)
где 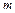 и
и 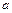 масса маятника и ускорение центра масс соответственно,
масса маятника и ускорение центра масс соответственно, 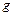 – ускорение свободного падения,
– ускорение свободного падения, 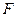 – сила натяжения нити. Уравнение вращательного движения для маятника имеет следующий вид:
– сила натяжения нити. Уравнение вращательного движения для маятника имеет следующий вид:
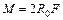 , (6.4)
, (6.4)
где 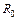 – радиус оси,
– радиус оси, 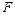 – сила натяжения одной нити. Поступательное и вращательное ускорения связаны соотношением:
– сила натяжения одной нити. Поступательное и вращательное ускорения связаны соотношением:
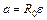 . (6.5)
. (6.5)
Поступательное ускорение маятника можно определить, измерив время опускания маятника 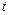 и расстояние
и расстояние 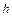 , которое он проходит за это время:
, которое он проходит за это время:
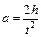 . (6.6)
. (6.6)
Из уравнений (6.2), (6.3), (6.4), (6.5) и (6.6) выразим момент инерции маятника Максвелла:
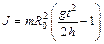 . (6.7)
. (6.7)
Дата добавления: 2015-06-17; просмотров: 621;
