Теоретическая часть. Во всех реальных механических процессах и системах имеют место силы трения, действие которых связывают в большинстве случаев с превращением механической

Во всех реальных механических процессах и системах имеют место силы трения, действие которых связывают в большинстве случаев с превращением механической энергии в тепло.

При перемещении одного тела относительно другого по его поверхности или слоев одного и того же тела относительно друг друга возникает сопротивление, характеризующееся рядом явлений, в том числе силой трения F_тр. Различают силу внешнего трения как силу сопротивления, тангенциальную относительно перемещения двух твердых тел при их соприкосновении, и силу внутреннего трения как силу сопротивления, тангенциальную относительно перемещения слоев среды относительно друг друга.

Характерной особенностью внешнего трения является наличие силы трения покоя, определяемой как предельная тангенциальная сила, под действием которой начинается относительное перемещение соприкасающихся тел. Внешнее трение возникает и между перемещающимися чистыми (ювенильными) поверхностями твердых тел, а также между поверхностями, покрытыми оксидными слоями. Практически трудно получить чистые поверхности. Оставшиеся или прилипшие адсорбированные поверхностно-активные молекулы образуют на поверхности так называемые граничные слои, сильно влияющие на процесс трения.

Основным законом для силы внешнего трения является закон Амонтона–Кулона, уточненный Б. В. Дерягиным:

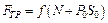(5.1)

где f – коэффициент трения скольжения, N – нормальная нагрузка, P₀ – удельная адгезия (сила прилипания, отнесенная к единице площади), S₀ – площадь истинного контакта.

Произведение 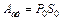называется тангенциальной адгезией. При отсутствии нагрузки сила трения равна А_ад и определяется молекулярными силами прилипания поверхностей – их адгезией. При малом значении величины тангенциальной адгезии закон для силы трения скольжения можно записать следующим образом:

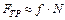. (5.2)

Сила трения скольжения определяется коэффициентом трения f. Экспериментальные данные показывают, что величина коэффициента трения не является константой, а зависит от материала поверхностей, их микрогеометрического профиля, смазки, газовой среды и многих других факторов.

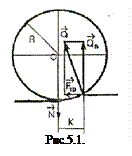
Трение качения возникает при перекатывании цилиндра или шара по поверхности твердого тела. Возникновение трения качения можно объяснить деформациями цилиндра и плоскости, имеющими место в реальных условиях. При этом могут возникать как упругие, так и пластические деформации. Из-за деформаций поверхностей линия действия силы реакции Q не совпадает с линией действия силы нормального давления N (рис. 5.1), в нашем случае равной весу катка. Нормальная составляющая Q_n этой реакции к плоскости практически равна приложенной нормальной нагрузке N, а горизонтальная составляющая представляет собой силу трения F_тр. Если цилиндр или шар движется по плоскости без ускорения, должно выполняться правило равенства моментов.

Момент силы трения качения относительно точки O равен произведению силы реакции опоры Q на расстояние смещения K вследствие контактных деформаций точки приложения:

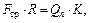(5.3)

где К – плечо силы, 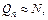R – радиус катка. Отсюда для силы трения качения получаем следующее выражение:

(5.4)

Величину K называют коэффициентом трения качения. Коэффициент трения качения, таким образом, представляет собой плечо силы Q_n и имеет размерность длины.

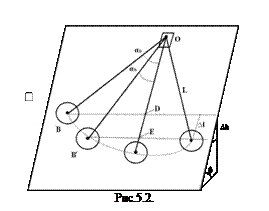В данной работе коэффициент трения качения шара по плоскости определяется методом наклонного маятника, предложенным А.С. Ахматовым. Шарик (рис. 5.2), подвешенный на нити, опирается на наклонную плоскость, угол наклона которой β, можно изменять. Если вывести шарик из положения равновесия, он начнет перекатываться по плоскости, при этом его движение имеет характер колебаний, затухающих главным образом под действием трения качения. Нормальная составляющая силы тяжести создает нормальное давление:

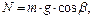(5.5)

где m – масса маятника.

Измерение силы трения с помощью наклонного маятника основано на измерении уменьшения амплитуды его колебаний за определенное число циклов. Формулу для расчета коэффициента трения можно получить, приравняв работе сил трения энергию ∆E_p, рассеянную за цикл колебаний маятника. За n циклов колебаний при переходе из положения B в положение B' (рис.5.2) маятник теряет энергию 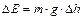, равную работе сил сопротивления на пройденном пути S:

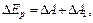(5.6)

где 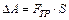– работа силы трения, ∆A₁ –- работа по преодолению сопротивления среды и трения в подвесе маятника, Dh – потеря высоты центром тяжести шарика. Пренебрегая ∆A₁ ввиду ее малости, имеем:

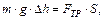(5.7)

После геометрических преобразований, очевидных из рисунка 5.2, учитывая формулы (5.3) и (5.4), имеем:

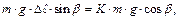(5.8)

где R – радиус шарика,

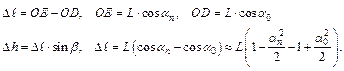
Если a₀ – амплитудное значение угла отклонения маятника в начальный момент, a_n – угол отклонения через n колебаний, L – длина маятника, то путь, который проходит центр тяжести маятника за n колебаний, равен 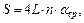где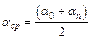

Учитывая геометрические соотношения для 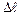, выразим коэффициент трения качения К из выражения (5.8):

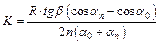. (5.9)

Получим значение коэффициента трения качения при малых углах a₀ и a_n (учитывая, что ):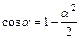

(5.10)

Здесь a₀ и a_n – углы, выраженные в радианах, n – число полных колебаний шарика. Учитывая (5.2) и используя методику, предложенную А.С.Ахматовым (метод наклонного маятника), можно получить формулу для расчета коэффициента трения скольжения f:

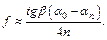(5.11)