Правила округления погрешностей
Погрешность обычно выражают одной значащей цифрой. Погрешности измерения указывают, какие цифры являются сомнительными в числовом значении измеренной величины. Так как точность измерения физической величины определяется измерением, а не вычислением, то округление числового значения результата измерения производится до цифр того же порядка, что и значение погрешности. При округлении результатов необходимо помнить следующие правила приближенных вычислений.
1. «Лишние» цифры у целых чисел заменяются нулями, а у десятичных дробей отбрасываются.
Например,
Y=123 357±687 (до округления),
Y=123 400±700 (после округления).
2. Если заменяемая нулем или отбрасываемая цифра меньше 5, то остающиеся цифры не изменяются, а если указанная цифра равна или больше 5, то последняя остающаяся цифра увеличивается на единицу.
Например,
Y=237.46±0.23 (до округления),
Y=237.5±0.2 (после округления).
Так как при  значение
значение 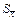 определяется с погрешностью более 30%, то величину погрешности необходимо округлить до двух значащих цифр, если первая из них единица, и до одной во всех остальных случаях. Например, а=1.35±0.16 м, b=1.4±0.3 м. Среднее арифметическое необходимо заканчивать в том же разряде, что и погрешность.
определяется с погрешностью более 30%, то величину погрешности необходимо округлить до двух значащих цифр, если первая из них единица, и до одной во всех остальных случаях. Например, а=1.35±0.16 м, b=1.4±0.3 м. Среднее арифметическое необходимо заканчивать в том же разряде, что и погрешность.
При сложении и вычитании приближенных чисел окончательный результат округляется так, чтобы он не имел значащих цифр в тех разрядах, которые отсутствуют хотя бы в одном из приближенных данных. При других математических операциях в результате необходимо оставить столько значащих цифр, сколько их осталось после операции сложения и вычитания в наименее точном числе.
Дата добавления: 2015-06-17; просмотров: 807;
