Измерительные приборы
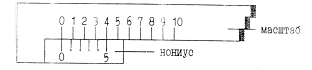 Рис. 1.1.
Рис. 1.1.
|
Измерение линейных величин (длин) обычно производится масштабной линейкой с сантиметровыми или миллиметровыми делениями. Для отсчета десятых и сотых долей миллиметра масштаб снабжают нониусом. Нониус – это небольшая линейка со шкалой, способная свободно перемещаться по масштабной линейке (рис. 1.1). Количество делений нониуса показывает, на сколько частей разделено одно деление основной шкалы (масштаба). В нашем примере одно деление масштаба разделено на пять делений. Следовательно, цена деления нониуса – 0,2 мм. Применим нониус для измерения диаметра цилиндра (рис.1.2). Если 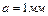 – цена деления масштаба,
– цена деления масштаба, 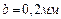 – цена деления нониуса, то диаметр определяется по формуле:
– цена деления нониуса, то диаметр определяется по формуле:
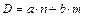 , (1.1)
, (1.1)
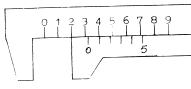 Рис. 1.2.
Рис. 1.2.
|
где: 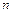 – число делений масштаба
– число делений масштаба 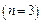 ,
, 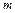 – число делений нониуса. Так как первое деление нониуса лучше всего совпадает с одним из делений основной шкалы, а именно с четвертым, то
– число делений нониуса. Так как первое деление нониуса лучше всего совпадает с одним из делений основной шкалы, а именно с четвертым, то 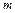 =1 и окончательно имеем
=1 и окончательно имеем 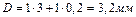 . В случае, когда ни одно из делений нониуса не совпадает в точности с каким-либо делением масштаба, в качестве
. В случае, когда ни одно из делений нониуса не совпадает в точности с каким-либо делением масштаба, в качестве 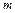 берут номер деления, которое ближе других подходит к одному из делений масштаба.
берут номер деления, которое ближе других подходит к одному из делений масштаба.
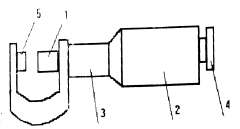 Рис. 1.3.
Рис. 1.3.
|
Нониусами снабжаются штангенциркули, теодолиты и многие другие приборы. Нониусы штангенциркулей изготовляются таким образом, что 1 мм основной шкалы делится на пять делений ( 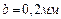 ), или на 10 делений (
), или на 10 делений ( 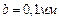 ), или на 20 делений (
), или на 20 делений ( 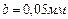 ).
).
Для еще более точных измерений линейных величин применяют микрометрические винты – винты с малым и точно выдержанным шагом. Такие винты используются, например, в микрометрах (рис. 1.3).
Измеряемое тело помещается между стержнями 1 и 5. Полный оборот барабана 2 с помощью ручки 4 перемещает стержень на 0,5 мм. Так как на барабан нанесено 50 делений, то цена деления барабана равна 0,01 мм. Основная шкала 3 имеет цену деления 0,5 мм, т.е. расстояние между соседними штрихами (нижним и верхним) равно 0,5 мм. Измеренное значение находится также по формуле (1.1), где 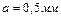 ;
; 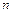 – число нижних и верхних штрихов основной шкалы, не закрытых барабаном (нулевой штрих не считается);
– число нижних и верхних штрихов основной шкалы, не закрытых барабаном (нулевой штрих не считается); 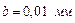 ;
; 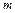 – номер штриха на барабане, который совпадает с осевой линией основной шкалы (или наиболее близок к ней).
– номер штриха на барабане, который совпадает с осевой линией основной шкалы (или наиболее близок к ней).
Методика эксперимента и обработка результатов измерений
1. Зарисовать таблицу 1.1. Измерить пять раз (в различных местах) микрометром диаметр и штангенциркулем высоту цилиндра. Результаты измерения занести в таблицу.
Таблица 1.1
| № | 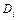 , мм , мм
| 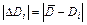 ,
мм ,
мм
| 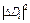
| 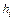 , мм , мм
| 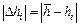 ,
мм ,
мм
| 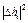
|
| 1. 2. 3. 4. 5. | ||||||
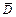 = =
| 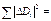
| 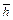 = =
| 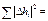
|
2. Найти средние значения результатов прямых измерений величин 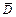 и
и 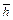 , вычислить
, вычислить 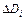 и
и 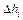 . Результаты занести в таблицу.
. Результаты занести в таблицу.
3. Оценить случайные, систематические и полные погрешности результатов прямых измерений величин. Записать окончательные результаты прямых измерений.
4. Вычислить объем цилиндра, т.е. найти результат косвенного измерения величины 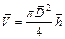 , оценить абсолютную и относительную погрешности косвенного измерения величины
, оценить абсолютную и относительную погрешности косвенного измерения величины 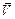 и записать для нее окончательный результат.
и записать для нее окончательный результат.
5. Сделать вывод по результатам работы.
Контрольные вопросы
1. Как производятся измерения штангенциркулем и микрометром?
2. Как находятся результаты прямых и косвенных измерений величин?
3. Как производится оценка погрешностей прямых и косвенных измерений?
4. Что такое доверительная вероятность и доверительный интервал?
5. Как записывается окончательный результат?
6. Получите формулу для вычисления абсолютной и относительной погрешностей объема цилиндра.
Дата добавления: 2015-06-17; просмотров: 973;
