Методика эксперимента, вывод формул

1. Вывод формулы зависимости скорости пули от ее массы. Выбрав пулю массы 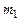, зарядим пистолет, сжав его пружину. При этом
в пружине будет запасена потенциальная энергия

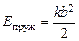, (1.1)

где 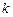– коэффициент упругости пружины, 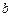– деформация пружины.

Предположим, что вся энергия сжатой пружины при выстреле полностью превращается в кинетическую энергию пули. Это означает, что мы пренебрегаем потерями энергии на преодоление трения между пулей и стволом пистолета и на сообщение кинетической энергии самой пружине. Учтем, кроме того, что геометрические размеры всех пуль одинаковы, а значит, одинакова деформация пружины для любой пули и, следовательно, одинакова запасаемая пружиной потенциальная энергия. Тогда из закона сохранения механической энергии следует, что пули различных масс , вылетая из пружинного пистолета, должны иметь одинаковые кинетические энергии

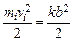, (1.2)

где 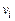– скорость i-й пули после выстрела.

Из (1.2) получаем зависимость скорости пули после выстрела от ее массы

. (1.3)

Поскольку величины 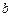и 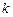для всех пуль одинаковы, то график ожидаемой зависимости скорости пули 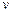от 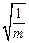должен согласно формуле (1.3) представлять собой прямую линию, проходящую через начало координат.

2. Вывод рабочей формулы. Пролетев небольшое расстояние между пистолетом и маятником, пуля входит в пластилин, заполняющий цилиндр, и за счет вязкого трения быстро теряет скорость. При этом часть механической энергии пули расходуется на неупругую деформацию и превращается во внутреннюю энергию пластилина и пули, т. е. пластилин и пуля нагреваются. Такой удар пули и маятника, в результате которого они начинают двигаться как единое целое, называется абсолютно неупругим. Механическая энергия в процессе такого удара не сохраняется (убывает).

Процесс удара – кратковременный. Если масса маятника достаточно велика по сравнению с массой пули ( 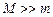), то за время удара он в силу своей инерционности не успевает выйти из положения равновесия. Это позволяет считать систему маятник–пуля в момент удара замкнутой в горизонтальном направлении, так как сила тяжести и сила натяжения подвеса направлены вертикально при вертикальном положении маятника. Для замкнутой системы можно применить закон сохранения импульса

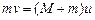, (1.4)

где 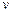– скорость пули до удара (при этом скорость маятника равна нулю); 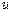– скорость, приобретенная системой маятник–пуля сразу после удара.

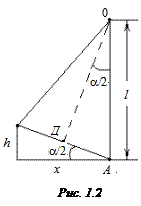Маятник вместе с пулей, получив за счет неупругого удара импульс, отклоняется от положения равновесия на угол 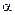. В процессе отклонения на маятник действуют сила тяжести (вниз) и сила упругости подвеса (перпендикулярно направлению мгновенной скорости маятника). Если пренебречь потерями энергии на трение в подвесе и на сопротивление воздуха, то работу при отклонении маятника совершает только гравитационная сила. Это позволяет воспользоваться законом сохранения механической энергии

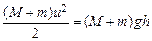, (1.5)

где 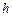– наибольшая высота, на которую поднимается маятник (рис. 1.2). Слева в формуле (1.5) стоит кинетическая энергия при поступательном движении маятника сразу после удара (в этой точке потенциальную энергию принимаем равной нулю), а справа – потенциальная энергия системы в момент ее остановки на высоте .

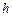Выразим высоту 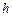через соответствующее горизонтальное смещение маятника 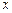, которое удобнее измерять. Предположим, что угол отклонения маятника от положения равновесия 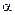мал. Из рис. 1.2 видно, что

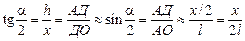, (1.6)

где – длина нити подвеса.

Из (1.6) получаем

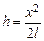. (1.7)

Уравнения (1.4), (1.5) и (1.7) образуют систему, решая которую получим скорость пули 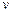перед ударом

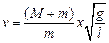. (1.8)

По выражению (1.8), осуществив прямые измерения смещения маятника 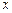и зная значения остальных величин, входящих в эту рабочую формулу, определим скорость пули 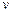путем косвенных измерений. Измерив скорости 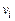для пуль с разными массами можно, следовательно, убедиться в справедливости теоретической зависимости (1.3).

3. Вывод формулы для определения погрешности косвенных измерений скорости 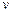. Методика оценки истинных значений и погрешности при прямых и косвенных измерениях изложена в [1].

Проведя прямые многократные измерения смещения маятника 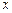для одной и той же пули (см. задание к работе) можно (см. [1]) оценить истинное значение 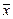и доверительную погрешность 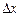этой величины, записав результат в виде 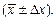Истинные значения остальных аргументов рабочей формулы (1.8) и их доверительные погрешности определены заранее и указаны в таблице исходных данных, помещенной около установки, и в Приложении. Подставляя истинные значения аргументов в рабочую формулу (1.8), получаем оценку истинного значения скорости пули

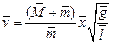, (1.9)

где черта означает оценку истинного значения.

Теперь (см. [1]) можно оценить доверительную абсолютную погрешность этой величины. В формуле (1.8) пять аргументов ( 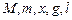), каждый из которых определен с некоторой погрешностью. Следовательно, формула для определения абсолютной погрешности скорости пули имеет вид

. (1.10)

Пользуясь формулой (1.8), вычислим частные производные от скорости по каждому из аргументов. В результате получим следующее выражение

. (1.11)

В формулу (1.11) входит пять квадратичных членов, каждый из которых определяет вклад погрешности одного из пяти аргументов формулы (1.8) в погрешность величины 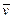. Прежде чем применять формулу (1.11), следует отдельно вычислить (приближенно) каждый из пяти квадратичных членов, чтобы сравнить их друг с другом. Сравнение покажет, точность определения каких аргументов мало влияет на абсолютную погрешность скорости. Эти члены из формулы (1.11) надо исключить, и только после этого, применив (1.11), получить оценку погрешности скорости 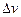. Численные результаты, полученные с помощью формул (1.9) и (1.11), записываются в виде

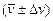м/с. (1.12)