И момента сил сопротивления

Для расчета движения механической системы маятник–груз применим уравнение динамики поступательного движения для груза, закрепленного на нити, и уравнение динамики вращательного движения для маятника.

Груз массой 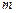движется с ускорением 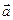под действием результирующей сил тяжести 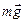и силы натяжения нити 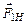(рис. 3.2). Запишем для груза второй закон Ньютона в проекции на направление движения

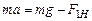(3.1)

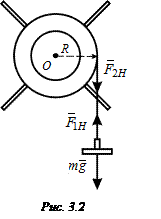Сила натяжения передается нитью от груза к шкиву вращающегося маятника. Если предположить, что нить невесомая, то на шкив маятника действует сила 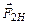, равная по величине 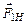и противоположная ей по направлению (следствие третьего закона Ньютона: 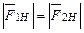). Сила натяжения создает вращательный момент 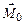относительно горизонтальной оси O, направленный вдоль этой оси «от нас» и приводящий в движение маятник Обербека. Величина этого момента равна 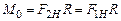, где 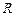– радиус шкива, на который намотана нить, 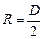, где 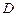– диаметр шкива.

Момент силы сопротивления относительно оси вращения 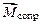направлен «к нам», т. е. в противоположную по отношению к вращательному моменту сторону.

Запишем для маятника основной закон динамики вращательного движения

,

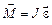где 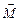– результирующий момент сил; 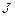– момент инерции маятника; 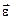– угловое ускорение.

В скалярной форме это уравнение имеет вид (записаны проекции векторов моментов сил и углового ускорения на ось вращения О,направление которой выбрано «от нас»)

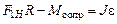. (3.2)

Используя кинематическую связь линейного и углового ускоре-
ния 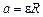, а также уравнение движения груза при нулевой начальной

скорости 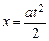, выразим 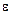через измеряемые величины 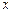и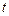

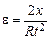. (3.3)

Решим систему уравнений (3.1) и (3.2), для чего умножим (3.1) на 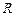и прибавим к (3.2)

.

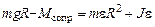Выражаем момент инерции маятника Обербека

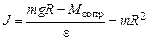. (3.4)

Все величины, кроме 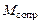, входящие в это уравнение, известны. Поставим задачу экспериментального определения .

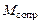Пусть J – момент инерции маятника Обербека без грузов. Из (3.4) следует, что

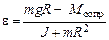. (3.5)

В условиях эксперимента 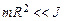, что позволяет считать зависимость e(m)линейной.

Эту зависимость можно использовать для экспериментальной оценки величины 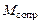. Действительно, если полученную экспериментально зависимость 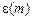экстраполировать до пересечения с осью абсцисс, т. е. до точки 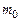на этой оси, для которой выполняется (см. 3.5) равенство 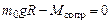, то это позволит определить 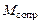как

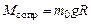. (3.6)

Для определения момента инерции маятника J воспользуемся (3.4), где величина 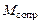предварительно определена из измерений e(m) и формулы (3.6). Подставив выражение e из (3.3) и 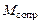из (3.6) в (3.4), получим рабочую формулу для определения момента инерции маятника

.

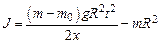Для используемого в работе маятника Обербека справедливо неравенство 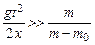. Учитывая это, получаем

.

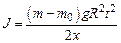Для расчетов удобно представить момент инерции в виде

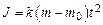, (3.7)

где .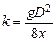

Для определения момента инерции маятника необходимо измерить время 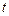опускания груза массой 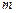на расстояние .

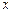Зависимость момента инерции маятника

от расстояния грузов до оси вращения

Момент инерции маятника Обербека может быть представлен как сумма моментов инерции барабана со стержнями ( 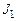) и моментов инерции четырех грузов массой 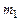, закрепленных на расстояниях r от оси вращения ( 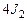). Если размеры этих грузиков малы по сравнению с , то их можно считать материальными точками. Для материальной точки момент инерции равен 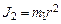. Тогда момент инерции маятника

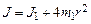. (3.8)

Эту зависимость момента инерции от расстояния грузов до оси вращения предполагается проверить, используя результаты опытов, полученные по формуле (3.7).

Значение 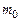можно взять из данных эксперимента для определения момента инерции маятника Обербека без грузов, считая, что момент сил сопротивления остается постоянным.