Тормозящей силы
Для оценки момента тормозящей силы воспользуемся энергетическими соотношениями. Поскольку силы трения являются диссипативными, то работа тормозящей силы Ат при переходе системы тело–груз из начального состояния в конечное равна
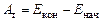 , (4.1)
, (4.1)
где 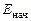 – механическая энергия системы тело–груз в начальном состоянии;
– механическая энергия системы тело–груз в начальном состоянии; 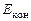 – механическая энергия системы тело–груз в конечном состоянии.
– механическая энергия системы тело–груз в конечном состоянии.
Механическая энергия системы складывается из кинетической и потенциальной энергий. В те моменты времени, когда система покоится, кинетическая энергия равна нулю и, следовательно, механическая энергия становится равной только потенциальной энергии системы. Такие состояния системы возникают в начальный момент времени, когда груз находится на отметке 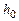 , и в тот момент, когда, опустившись вниз, груз за счет вращения тела поднимается до отметки
, и в тот момент, когда, опустившись вниз, груз за счет вращения тела поднимается до отметки 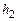 (рис. 4.1). Если принять, что на высоте
(рис. 4.1). Если принять, что на высоте 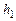 потенциальная энергия груза равна нулю, то приращение механической энергии для выбранных начального и конечного состояний системы равно
потенциальная энергия груза равна нулю, то приращение механической энергии для выбранных начального и конечного состояний системы равно
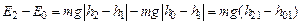 , (4.2)
, (4.2)
где 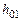 – расстояние между отметками
– расстояние между отметками 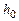 и
и 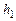 ;
; 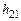 – расстояние между отметками
– расстояние между отметками 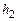 и
и 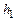 .
.
Будем считать, что момент тормозящей силы в основном связан с вращательным движением тела, т. е. тормозящей силой, действующей на груз, пренебрежем. Тогда элементарная работа момента тормозящей силы равна скалярному произведению
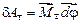 ,
,
где 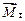 – вектор момента тормозящей силы;
– вектор момента тормозящей силы; 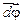 – вектор бесконечно малого углового перемещения тела.
– вектор бесконечно малого углового перемещения тела.
Оба вектора 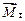 и
и 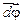 направлены вдоль оси вращения, но в про-тивоположные стороны. Следовательно,
направлены вдоль оси вращения, но в про-тивоположные стороны. Следовательно,
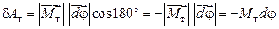 .
.
Тогда полная работа момента тормозящей силы, если предположить, что он постоянен, равна
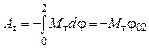 , (4.3)
, (4.3)
где 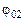 – угол поворота тела вокруг оси при переходе системы из начального состояния в конечное (груз при этом перемещается от отметки
– угол поворота тела вокруг оси при переходе системы из начального состояния в конечное (груз при этом перемещается от отметки 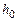 до отметки
до отметки 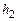 ).
).
При движении груза вниз от отметки 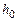 до отметки
до отметки 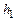 со шкива сматывается нить длиной
со шкива сматывается нить длиной 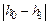 . Учитывая, что длина окружности шкива равна
. Учитывая, что длина окружности шкива равна 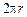 и каждый оборот шкива соответствует углу
и каждый оборот шкива соответствует углу 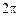 радиан, найдем угол поворота шкива при движении груза вниз
радиан, найдем угол поворота шкива при движении груза вниз
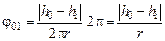 [рад]. (4.4)
[рад]. (4.4)
Очевидно, что при дальнейшем вращении тела до момента, когда груз остановится на отметке 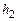 , оно повернется на угол
, оно повернется на угол
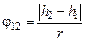 [рад].
[рад].
Тогда общий угол поворота тела, соответствующий переходу груза от отметки 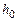 до отметки
до отметки 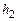 , равен
, равен
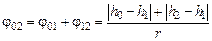 [рад]. (4.5)
[рад]. (4.5)
Подставляя (4.2) и (4.3) в (4.1), получаем
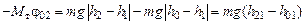 .
.
Отсюда, используя (4.5), получаем формулу для оценки модуля вектора момента тормозящей силы
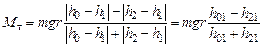 . (4.6)
. (4.6)
Дата добавления: 2015-06-17; просмотров: 1227;
