Момента инерции тела с учетом момента тормозящей силы

Рассмотрим систему тело–груз в начальный момент времени, когда груз находится на отметке 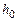, а в качестве конечного выберем тот момент времени, когда груз опустился до нижней отметки 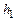, соответствующей полной длине нити. Опять будем исходить из энергетического соотношения (4.1).

Для выбранных начального и конечного состояний получим

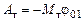, (4.7)

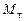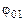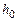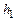где – момент тормозящей силы (4.6); – угол поворота тела, соответствующий перемещению груза от отметки до (4.4).

Начальная механическая энергия системы тело–груз равна

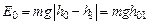. (4.8)

Конечная механическая энергия системы складывается из кинетической энергии вращательного движения тела и кинетической энер-
гии поступательного движения груза в момент прохождения им от-
метки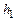

,

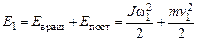где 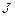– момент инерции тела; 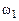– угловая скорость вращения тела в момент 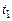(см. рис. 4.1); 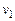– скорость поступательного движения груза в момент .

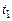Строго говоря, в процессе движения груз за счет упругого растяжения нити опускается чуть ниже отметки 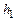, тормозится нитью, а затем за счет упругого сжатия нити возвращается на эту отметку.

Предполагая, что движение системы является равноускоренным, для скорости груза на отметке 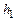получаем

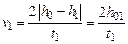, (4.10)

где 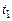– время, за которое груз опустится от отметки 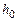до .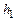

Угловая скорость вращения тела в тот же момент времени равна

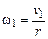, (4.11)

где – радиус шкива, на который намотана нить.

Подставляя (4.7) – (4.9) в (4.1), получаем

.

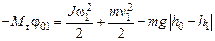Из этой формулы, учитывая (4.4), (4.10) и (4.11), выражаем момент инерции :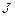

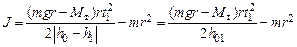, (4.12)

где 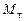– момент тормозящей силы, который вычисляется по форму-
ле (4.6).