МОМЕНТЫ ЯДЕР

Спин. Важнейшей величиной для элементарных частиц является собственный механический момент или спин. Макроскопическим аналогом элементарной частицы является вращающееся вокруг своей оси тело – волчок. Естественной единицей механического момента в микромире является величина 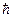. Однако спин многих элементарных частиц равен 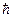/2. Полуцелая величина встречается только как спин элементарной частицы. Более того, собственно элементарными частицами как раз являются частицы со спином ½, тогда как частицы с целочисленным спином 1 или 0 оказываются вспомогательными, носителями взаимодействий собственно элементарных частиц.

Поскольку нуклоны обладают собственными механическими моментами, или спинами равными 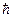/2, то и ядра должны иметь механические моменты. Кроме того, нуклоны в ядре участвует в орбитальном движении, которое также характеризуется определенным моментом количества движения каждого нуклона. Орбитальные моменты принимают только целочисленные значения 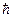. Все механические моменты нуклонов, как спины, так и орбитальные, суммируются алгебраически и составляют механический момент, или спин, ядра I.

Несмотря на то, что число нуклонов в ядре может быть очень большим, спины ядер обычно невелики и составляют не более нескольких единиц 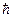. Это определяется особенностью взаимодействия одноименных нуклонов. Все парные протоны, а также парные нейтроны взаимодействуют так, что их спины взаимно компенсируются, т.е. пары протонов и нейтронов всегда взаимодействуют с антипараллельными спинами. Более того, суммарный орбитальный момент пары протонов и нейтронов также всегда равен нулю. В результате ядра, состоящие из четного числа протонов и четного числа нейтронов (четно-четные ядра), не имеют механического момента, их спин I=0. Отличные от нуля спины имеют только ядра, имеющие непарные протоны или нейтроны. Если имеется один непарный нуклон, то его спин суммируется с его же орбитальным моментом и спин ядра четно-нечетного или нечетно-четного имеет полуцелое значение: 1/2, 3/2, 5/2 и т.д.. Ядра нечетно-нечетные имеют целочисленные спины: 1, 2, 3 и т.д.

Магнитный момент. Имеющая спин электрически заряженная частица обязана иметь и магнитный момент. Магнитный момент электрона оказался равным магнетону Бора (1.7). Магнитный момент протона вопреки ожиданию аналогии с электроном отличается от значения ядерного магнетона

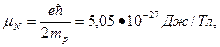(2.4)

являющегося единицей магнитного момента частицы с массой покоя протона 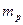(1.7) и равен:

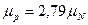. (2.5)

При измерении магнитных моментов ядер атомов было обнаружено, что и нейтрон, не имеющий электрического заряда, также должен иметь магнитный момент. Специальные эксперименты подтвердили, что у нейтрона есть магнитный момент, и он оказался равным:

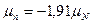. (2.6)

Знак минус соответствует направлению вектора магнитного момента против вектора спина, что имеет место и для электрона, тогда как плюс – по направления вектора спина. Для классического заряженного тела знак минус означает магнитный момент, образованный вращением отрицательного заряда, а знак плюс – вращением положительного заряда.

Численные значения магнитных моментов нуклонов, а также наличие магнитного момента у нейтрона не находят простого объяснения и, возможно, обязаны сложной структуре этих частиц.

Магнитные моменты ядер измеряются в ядерных магнетонах 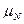(2.4) и у разных ядер равны от -2 до +5 ядерных магнетонов. Из-за относительно большой массы нуклонов магнитные моменты ядер очень малы по сравнению с магнитным моментом электрона. Поэтому определение магнитных моментов ядер намного сложнее соответствующих измерений для электронов. Магнитные моменты ядер измеряются, как и спины, при спектроскопических измерениях, однако наиболее точным методом является метод ядерного магнитного резонанса. Магнитный момент четно-четных ядер, как и спин, равен нулю. Магнитные моменты ядер с непарными нуклонами образуются собственными магнитными моментами этих нуклонов, а также магнитным моментом, связанным с орбитальным движением непарного протона. Вместе с тем большинство измеренных магнитных моментов может быть объяснено лишь с учетом вклада в магнитный момент ядра движения многих нуклонов, не входящих в заполненные нуклонные оболочки.

Электрический квадрупольный момент. Атомные ядра, спин которых 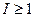, имеют отличные от нуля квадрупольные моменты, что говорит об их неточно сферической форме. Квадрупольный момент имеет знак плюс, если ядро вытянуто в плоскости вдоль оси спина (веретенообразное тело), и знак минус, если ядро растянуто в плоскости перпендикулярной оси спина (чечевицообразное тело). Известны ядра с положительными и отрицательными квадрупольными моментами. Ядро, обладающее квадрупольным моментом, создает несферически симметрическое электрическое поле, что приводит к образованию дополнительных энергетических уровней атомных электронов и появлению в спектрах атомов линий сверхтонкой структуры, расстояния между которыми зависят от квадрупольного момента.