Сложение вращений тела вокруг двух осей

На рис. 54 изображено тело, которое со­вершает сложное движение – вращение вокруг оси, которая сама вращается вокруг другой, не­подвижной оси. Естественно, первое вращение следует на­звать относительным движением тела, второе – переносным, а соответствующие оси обозна­чить 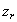и .

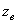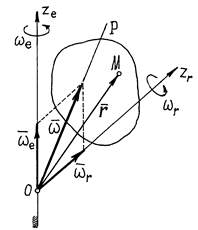
Рис.54

Абсолютным движением будет вращение вокруг точки пересечения осей О. (Еcли тело имеет больший размер, то его точка, совпа­дающая с О, все время будет неподвижной). Угловые скорости переносного вращения и от­носительного вращения изображается векто­рам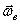и и 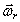, отложенными из неподвижной точки О, точки пересечения осей, по соответст­вующим осям.

Найдем абсолютную скорость какой-нибудь точки М тела, положение которой определяется радиусом-вектором 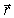(рис.54).

Как известно, она складывается из двух скоростей, относительной и переносной: 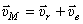. Но относительное движение точки (ис­пользуя правило остановки), есть вращение с угловой скоро­стью 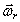вокруг оси 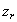, определяется радиусом-вектором 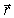. Поэтому, .

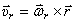Переносное движение точки в данный момент времени, опять используя правило остановки, тоже есть вращение, но вокруг оси 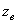с угловой скоростью 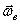и будет определяться тем же радиусом-вектором 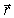. Поэтому и переносная скорость .

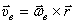Абсолютная же скорость, скорость при вращении вокруг неподвижной точки О, при сферическом движении, определяется аналогично 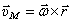, где 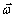- абсолютная угловая скорость, направленная по мгновенной оси вращения Р.

По формуле сложения скоростей получим: 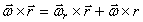или .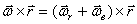

Отсюда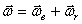

То есть мгновенная угловая скорость, угловая скорость абсолютного движения, есть векторная сумма угловых скоростей переносного и относительного движений. А мгновенная ось вращения P, направленная по вектору 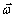, совпадает с диагональю параллелограмма, построенного на векторах 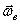и 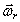(рис.54).

Частные случаи:

1. Оси вращения 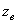и 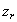параллельны, на­правления вращений одинаковы (рис. 55).

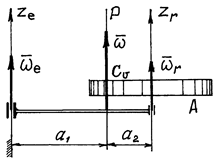
Рис.55

Так как векторы 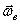и 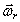параллельны и направлены в одну сторону, то абсолютная угловая скорость по величине равна сумме их модулей 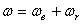и вектор ее направлен в туже сторону. Мгновенная ось вращения Р делит рас­стояние между осями на части обратно пропорциональные 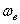и :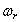

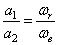. (Аналогично равнодействующей параллельных сил).

В этом частном слу­чае тело А совершает плоскопараллельное движение. Мгновенный центр скоростей 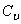находится на оси Р.

2. Оси вращения параллельны, направления вращений противоположны (рис.56).

Рис.56

В этом случае 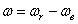(при 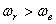). Мгновенная ось вращения и мгновенный центр скоростей находятся за вектором большей угловой скорости на расстояниях таких, что 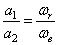(опять по аналогии определения равнодействующей параллельных сил).

3. Оси вращения параллельны, направления вращений противоположны и угловые скорости равны.

Угловая скорость абсолютного движения 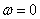и, следовательно, тело совершает поступательное движение. Этот случай называется парой вращений, по аналогии с парой сил.

Пример 16. Диск радиусом R вращается вокруг горизонтальной оси с угловой скоростью 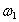, а эта ось вместе с рамкой вращается вокруг вертикальной неподвижной оси с угловой скоростью 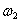(рис.57).

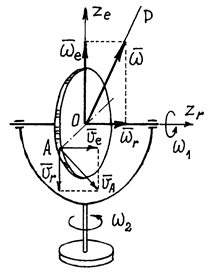
Рис.57

Горизонтальная ось – это ось относительного вращения 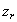; вертикальная ось – ось переносного вращения 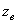. Соответственно угловые скорости 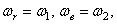векторы их направлены по осям 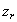и .

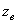Абсолютная угловая скорость 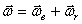, а величина ее, так как ,

.

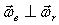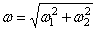Скорость точки А, например, можно найти или как сумму переносной и относи­тельной скоростей: 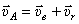, где

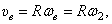
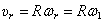и ,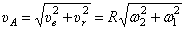

или как при абсо­лютном движении, при вращении вокруг мгновенной оси Р, .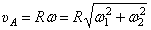

Вектор скорости 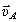будет расположен в плоскости перпендикулярной вектору 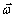и оси Р.

Пример 17. Водило ОА с укрепленными на нем двумя колесами 2 и 3 вращается вокруг оси О с угловой скоростью 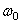. Колесо 2 при этом будет обкатываться по неподвижному колесу 1 и заставит вращаться колесо 3. Найдем угловую скорость 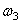, этого колеса. Радиусы колес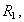 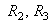(рис. 58).

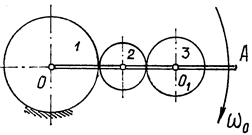
Рис.58

Колесо 3 участвует в двух движениях. Вращаться вместе с водилом вокруг оси О и относительно оси 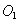. Ось О будет переносной осью, ось 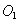– относительной. Переносная угловая скорость колеса 3 – это угловая скорость водила 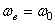, направленная по часовой стрелке, как .

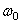Чтобы определить угловую скорость относительного движения, наблюдателю нужно находиться на водиле. Он увидит водило неподвижным, колесо 1 вращающимся против часовой стрелки со скоростью 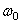(рис. 59), а колесо 3 – вращающимся с относительной угловой скоростью 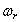, против часовой стрелки. Так как 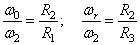, то 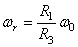. Оси вращения параллельны, направления вращений противоположны. Поэтому 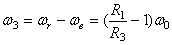и направлена так же как 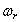, против часовой стрелки. 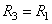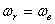В частности, если , то и 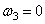.Колесо 3 будет двигаться поступательно.

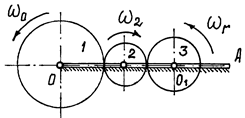
Рис.59

Исследование движения других подобных конст­рукций (планетарных и дифференциальных редукто­ров, передач) ведется аналогичным способом.

Переносной угловой скоростью является угловая скорость водила (рамки, крестовины и т.п.), а чтобы определить относительную скорость какого-либо ко­леса, нужно водило остановить, а неподвижное колесо за­ставить вращаться с угловой скоростью водила, но в противоположную сторону.

Угловые ускорения тела в абсолютном движении можно искать как производную 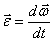, где 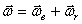. Покажем (рис.60) единичные векторы 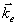и 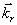(орты осе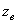й и 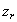), а векторы угловых скоростей запишем так: , .

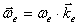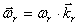Тогда 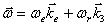и угловое ускорение, при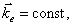

.

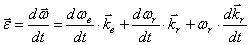Здесь 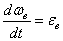, 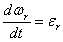и .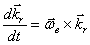

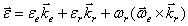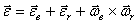Поэтому или

и ,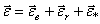

где 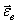– угловое ускорение переносного вращения; 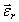– угловое ускорение относительного вращения; 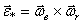– добавочное угловое ускорение, которое определяет изменение относительной угловой скорости 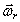при переносном движении. Направлен этот вектор перпендикулярно осям 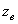и 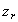, как скорость конца вектора 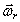. Модуль добавочного углового ускорения 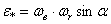, где 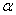- угол между осями.

Конечно, если оси вращения параллельны, это угловое ускорение 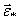будет равно нулю, так как .

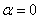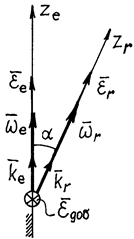
Рис.60