Поле двухпроводной линии над поверхностью земли
Для расчета поля введем две дополнительные оси. Определим потенциал произвольной точки M (рис. 15.14).
 |
Согласно (15.30) потенциал произвольной точки от заряженной оси
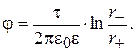
В данном случае
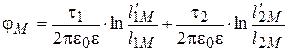
или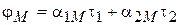 
, (15.37)
где a1M и a2M – потенциальные коэффициенты, зависящие от характера среды и расположения проводов.
Уравнение (15.36) показывает, что потенциал прямо пропорционален заряду.
Потенциалы проводов можно записать в виде
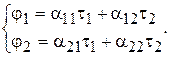(15.38)
Эти уравнения называются первой группой формул Максвелла.
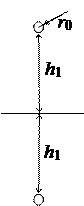С учетом расстояний, показанных на рис. 15.15, потенциальные коэффициенты можно определить по формулам:
|
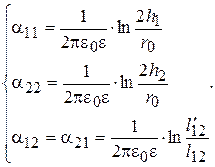(15.39)
Коэффициент a11 численно равен потенциалу j1, когда на первом проводе находится единичный заряд, а на других проводах заряд отсутствует.
Коэффициент a12 численно равен потенциалу j1, когда на втором проводе находится единичный заряд, а на других проводах заряд отсутствует.
Аналогично можно описать другие потенциальные коэффициенты.
Решив систему (15.37) относительно зарядов, получим вторую группу формул Максвелла.
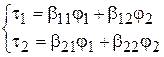(15.40)
Коэффициенты b называют емкостными коэффициентами. Их размерность обратна размерности потенциальных коэффициентов. Коэффициенты с одинаковыми индексами положительны, а с разными – отрицательны.
Если ввести частичные емкости между проводами линии и землей (рис. 15.16), то заряды можно записать в виде
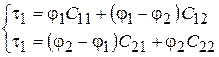
или
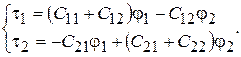(15.41)
 |
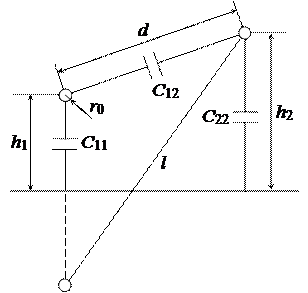Рис. 15.16. Частичные емкости линии
Емкости C11, C22 называются собственными частичными емкостями, C12 и C21 – взаимными частичные емкости.
Из сравнения систем (15.39) и (15.40) видно, что
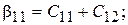
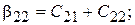
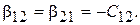
Откуда следует, что
,
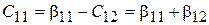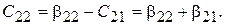
Если к проводам подведено напряжение U от незаземленного источника, то провода заряжаются так, что
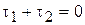, или 
.
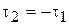В этом случае можно говорить о рабочей емкости линии
.
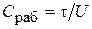Подставив значение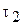 
в уравнение (15.41) получим
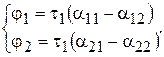
При этом рабочая емкость будет равна
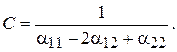(15.42)
Согласно (15.38)
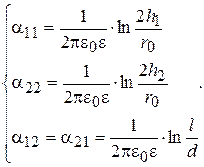
Подставив эти значения в (15.42) получим
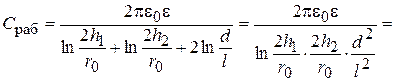
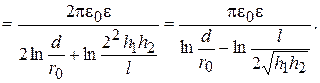(15.43)
Величина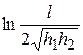 
определяет влияние земли на величину емкости.
(Так как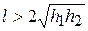 
, то близость земли увеличивает емкость системы двух проводов.)
Дата добавления: 2015-06-17; просмотров: 804;