Матрица жесткости КЭ
Известные в механике геометрические и физические соотношения для континуальных систем можно записать в виде, аналогичном рассмотренным ранее уравнениям дискретного подхода. Например,
для дискретной системы: для континуальной системы: 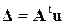 ,
, 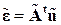 ,
, 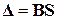 ,
, 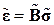 .
.
Здесь 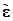 и
и 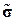 – вектора деформаций и напряжений, а
– вектора деформаций и напряжений, а 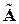 и
и 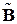 – матрицы равновесия и податливости континуальной системы. В отличие от дискретного подхода, уравнения континуального подхода удовлетворяются во всех точках системы.
– матрицы равновесия и податливости континуальной системы. В отличие от дискретного подхода, уравнения континуального подхода удовлетворяются во всех точках системы.
При рассмотрении конечного элемента как континуальной системы принцип Лагранжа 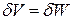 можно записать в виде
можно записать в виде
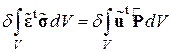 ,
,
где левая и правая части представляют возможные работы внутренних и внешних сил, а интегрирование ведется по объему КЭ V.
После этого осуществляется переход к дискретной модели КЭ с использованием матрицы форм H. Тогда после ряда преобразований получается матричное уравнение, связывающее вектор узловых перемещений u с вектором узловых усилий P КЭ:
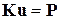 ,
,
в которой симметричная квадратная матрица
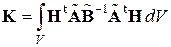
называется матрицей жесткости конечного элемента. Физический смысл элемента kij этой матрицы – это реакция (реактивная сила), возникающая в i-ом направлении отзаданного единичного перемещения в j-ом направлении.
К примеру, для рассмотренного ферменного КЭ, находящегося в одноосном напряженном состоянии, геометрическое уравнение будет 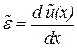 . Сравнив его с матричным уравнением
. Сравнив его с матричным уравнением 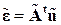 , видим, что матрица равновесия является дифференциальным оператором с одним членом, т.е.
, видим, что матрица равновесия является дифференциальным оператором с одним членом, т.е. 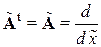 . Из уравнения связи между деформацией и напряжением
. Из уравнения связи между деформацией и напряжением 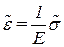 видно, что матрица податливости будет
видно, что матрица податливости будет 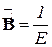 .
.
Для определения матрицы жесткости КЭ вычислим:
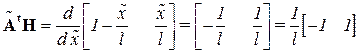 ,
,
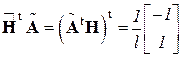 ,
, 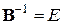 .
.
Интегрирование по объему V сводится к интегрированию по длине l КЭ, т.к. 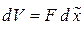 (F − площадь сечения КЭ). Тогда
(F − площадь сечения КЭ). Тогда
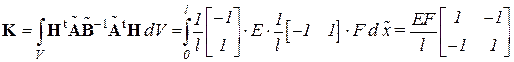 .
.
При рассмотрении прямоугольного КЭ толщиной t и размерами 2a и 2b с четырьмя узлами i, j, k, m и восемью узловыми перемещениями (рис. 14.4), матрица жесткости будет иметь размеры 8´8.
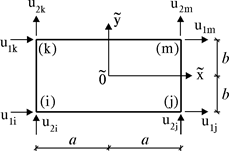
Рис. 14.4
Для краткости записи матрицу жесткости этого КЭ можно представить в блочной форме с 16 блоками одинаковой размерности 2´2:
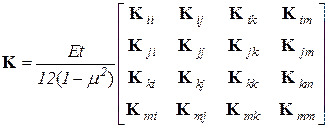 .
.
Здесь μ – коэффициент Пуассона. Элементы каждого блока матрицы K определяются по разным формулам. Например,
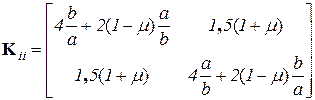 .
.
Дата добавления: 2015-06-17; просмотров: 985;
