Магнитное поле и его характеристики. Электрическое поле действует как на неподвижные, так и на движущиеся в нем электрические заряды
Электрическое поле действует как на неподвижные, так и на движущиеся в нем электрические заряды. Важнейшая особенность магнитного поля состоит в том, что оно действует только на движущиеся в этом поле электрические заряды. Ориентация контура в пространстве определяется направлением нормали к контуру. Направление нормали определяется правилом правого винта: за положительное направление нормали принимается направление поступательного движения винта, головка которого вращается в направлении тока, текущего в рамке.

За направление магнитного поля в данной точке принимается направление, вдоль которого располагается положительная нормаль к рамке. За направление магнитного поля может быть также принято направление, совпадающее с направлением силы, которая действует на северный полюс магнитной стрелки, помещенной в данную точку. Так как оба полюса магнитной стрелки лежат в близких точках поля, то силы, действующее на оба полюса, равны друг другу. Следовательно, на магнитную стрелку действует пара сил, поворачивающая ее так, чтобы ось стрелки, соединяющая южный полюс с северным, совпадала с направлением поля.
Рамкой с током можно воспользоваться также и для количественного описания магнитного поля. Так как рамка с током испытывает ориентирующее действие поля, то на нее в магнитном поле действует пара сил. Вращающий момент сил зависит как от свойств поля в данной точке, так и от свойств рамки и определяется формулой
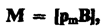 гдеpm–вектор магнитного момента рамки с током (В - вектор магнитной индукции,количественная характеристика магнитного поля). Для плоского контура с током I
гдеpm–вектор магнитного момента рамки с током (В - вектор магнитной индукции,количественная характеристика магнитного поля). Для плоского контура с током I 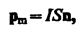 где S – площадь поверхности контура (рамки), n – единичный вектор нормали к поверхности рамки. Направление рm совпадает, таким образом, с направлением положительной нормали.
где S – площадь поверхности контура (рамки), n – единичный вектор нормали к поверхности рамки. Направление рm совпадает, таким образом, с направлением положительной нормали.
Если в данную точку магнитного поля помещать рамки с различными магнитными моментами, то на них действуют различные вращающие моменты, однако отношение Мmax/рm (Мmax – максимальный вращающий момент) для всех контуров одно и то же и поэтому может служить характеристикой магнитного поля, называемой магнитной индукцией: 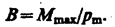
Магнитная индукция в данной точке однородного магнитного поля определяется максимальным вращающим моментом, действующим на рамку с магнитным моментом, равным единице, когда нормаль к рамке перпендикулярна направлению поля. Так как магнитное поле является силовым, то его, по аналогии с электрическим, изображают с помощью линий магнитной индукции – линий, касательные к которым в каждой точке совпадают с направлением вектора В. Их направление задается правилом правого винта: головка винта, ввинчиваемого по направлению тока, вращается в направлении линий магнитной индукции.

Линии магнитной индукции всегда замкнуты и охватывают проводники с током.
Магнитное поле макротоков описывается вектором напряженности Н. Для однородной изотропной среды вектор магнитной индукции связан с вектором напряженности следующим соотношением: 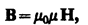 где m0 – магнитная постоянная, m - безразмерная величина – магнитная проницаемость среды, показывающая, во сколько раз магнитное поле макротоков Н усаливается за счет поля микротоков среды.
где m0 – магнитная постоянная, m - безразмерная величина – магнитная проницаемость среды, показывающая, во сколько раз магнитное поле макротоков Н усаливается за счет поля микротоков среды.
Сравнивая векторные характеристики электростатического (Е и D) и магнитного (В и Н) полей, укажем, что аналогом вектора напряженности электростатического поля Е является вектор магнитной индукции В, так как векторы Е и В определяют силовые действия этих полей и зависят от свойств среды. Аналогом вектора электрического смещения D является вектор напряженности Н магнитного поля.

2. Закон Био – Савара – Лапласа и его применение к расчету магнитного поля
Закон Био – Савара – Лапласа для проводника с током I, элемент dl которого создает в некоторой точке А индукцию поля dB, записывается в виде
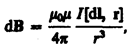 где dl – вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r– радиус-вектор, проведанный из элемента dl проводника в точку А поля, r — модуль радиуса-вектора r. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление dB, если поступательное движение винта соответствует направлению тока в элементе.
где dl – вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r– радиус-вектор, проведанный из элемента dl проводника в точку А поля, r — модуль радиуса-вектора r. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление dB, если поступательное движение винта соответствует направлению тока в элементе.
Модуль вектора dB определяется выражением
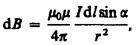
где a - угол между векторами dl и r.
Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:
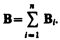
Расчет характеристик магнитного поля (В и Н) по приведенным формулам в общем случае сложен. Однако если распределение тока имеет определенную симметрию, то применение закона Био - Савара - Лапласа совместно с принципом суперпозиции позволяет просто рассчитать конкретные поля. Рассмотрим два примера.

Магнитное поле прямого тока – тока, текущего по тонкому прямому проводу бесконечной длины. В произвольной точке А, удаленной от оси проводника на расстояние R, векторы dB от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к вам»). Поэтому сложение векторов dB можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол a (угол между векторами dl и r), выразив через него все остальные величины.
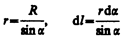
(радиус дуги CD вследствие малости dl равен r, и угол FDC по этой же причине можно считать прямым).
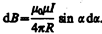
Так как угол a для всех элементов прямого тока изменяется в пределах от 0 до p, то, 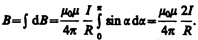
Следовательно, магнитная индукция поля прямого тока
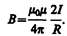
Магнитное поле в центре кругового проводника с током. Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления — вдоль нормали от витка. Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sina =1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то,
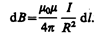
Тогда
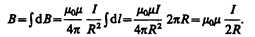
Следовательно, магнитная индукция поля в центре кругового проводника с током
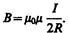

Дата добавления: 2015-06-17; просмотров: 1559;
