Угловая скорость и угловое ускорение
Угловой скоростью называется векторная величина, равная первой  производной угла поворота тела по времени:
производной угла поворота тела по времени: 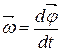 . Вектор
. Вектор 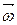 направлен вдоль оси вращения по правилу правого винта, т.е. так же, как и вектор
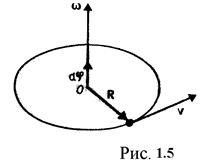
направлен вдоль оси вращения по правилу правого винта, т.е. так же, как и вектор 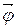 (рис.1.5).
(рис.1.5).
 Размерность угловой скорости – радиан в секунду (рад/с). Линейная скорость точки
Размерность угловой скорости – радиан в секунду (рад/с). Линейная скорость точки 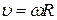 .
.
В векторном виде формулу для линейной скорости можно написать как векторное произведение: 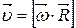 .
.
Если w = const, то вращение равномерное и его можно характеризовать периодом вращения T – временем, за которое точка совершает один полный оборот, т.е. поворачивается на угол 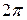 . Так как промежутку времени Δt = T соответствует
. Так как промежутку времени Δt = T соответствует 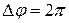 , то
, то 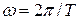 откуда
откуда 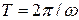 .
.
Число n полных оборотов, совершаемых телом при равномерном его движении по окружности за время t, называется частотой вращения:
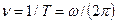 . Величину ω иногда называют циклической частотой, т.е. число оборотов за время 2π секунды
. Величину ω иногда называют циклической частотой, т.е. число оборотов за время 2π секунды 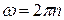 .
.
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени: 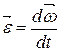 .
.
Размерность углового ускорения – рад/с2.
Тангенциальная составляющая ускорения связана с угловым ускорением по формуле 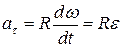 .
.
В случае равнопеременного движения точки по окружности ( 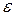 = const)
= const)
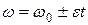 ,
, 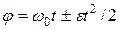 , где
, где 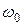 – начальная угловая скорость.
– начальная угловая скорость.
Дата добавления: 2015-06-17; просмотров: 1340;
