Равномерное движение точки по окружности
При таком движении (рис. 6.10)  и
и  , так как при равномерном движении
, так как при равномерном движении 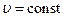 , а при движении по окружности
, а при движении по окружности  . Из формулы
. Из формулы 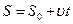 скорость равномерного движения по окружности
скорость равномерного движения по окружности
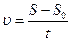 .
.
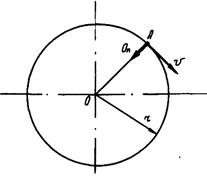
Рис. 6.10. Равномерное движение точки по окружности
Если принять t = Т – периоду, т. е. времени одного обхода точкой окружности, то 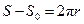 и
и
 или
или  ,
,
где 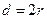 – диаметр окружности.
– диаметр окружности.
3. Равнопеременное движение. Если  , то движение точки называется равнопеременным.
, то движение точки называется равнопеременным.
Уравнение равнопеременного движения точки
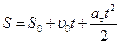 .
.
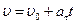 – скорость в любой момент времени.
– скорость в любой момент времени.
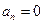 и
и 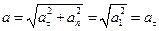 .
.
А. При равнопеременном прямолинейном движении, если не известно время t, получим первую вспомогательную формулу

Если не известно 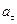 :
:
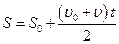 ,
,
где 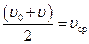 – средняя скорость точки при ее равномерном движении.
– средняя скорость точки при ее равномерном движении.
Б. Если равноускоренное движение точки начинается из начала отсчета траектории (S0 = 0) и без начальной скорости (  ), то предыдущие формулы приобретают более простой вид:
), то предыдущие формулы приобретают более простой вид:
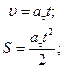
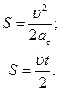
Примерами такого движения могут служить движение автомобиля при трогании с места или движение самолета на взлетной полосе, а также известное из физики свободное падение тел.
В. При свободном падении 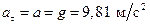 . В этом случае, если в формулах из пункта (Б) S заменить высотой падения Н, то формулы примут вид
. В этом случае, если в формулах из пункта (Б) S заменить высотой падения Н, то формулы примут вид

Предпоследняя из этих формул, представленная в виде  , называется формулой Галилея.
, называется формулой Галилея.
Глава 7. Простейшие движения твердого тела
7.1. Поступательное движение
Движение твердого тела, при котором любой выбранный в теле отрезок прямой перемещается, оставаясь параллельным своему первоначальному положению, называется поступательным.
Рассмотрим две точки А и В, соединенные отрезком АВ (рис. 7.1). Очевидно, что при перемещении отрезка АВ параллельно первоначальному положению (  ) точки A и В движутся по одинаковым траекториям, т. е. если траекторию
) точки A и В движутся по одинаковым траекториям, т. е. если траекторию 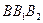 совместить с траекторией
совместить с траекторией  , то они совпадут. Если вместе с точкой A рассмотреть движение точки C, то при движении тела отрезок АС также остается параллельным своему первоначальному положению (
, то они совпадут. Если вместе с точкой A рассмотреть движение точки C, то при движении тела отрезок АС также остается параллельным своему первоначальному положению ( 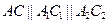 ) и траектория точки C (кривая
) и траектория точки C (кривая  ) одинакова с траекториями
) одинакова с траекториями  и
и 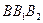 :
:
 , или
, или 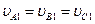 , или
, или  ;
;
 , или
, или 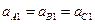 , или
, или  .
.

Рис. 7.1. К анализу поступательного движения твердого тела
Как видим, поступательное движение твердого тела полностью характеризуется движением любой его точки. Обычно поступательное движение тела задается движением его центра тяжести, иначе говоря, при поступательном движении тело можно считать материальной точкой.
Примерами поступательного движения тел могут служить какой-либо ползун 1, движущийся в прямолинейных направляющих 2 (рис. 7.2, а), или прямолинейно движущийся автомобиль (вернее, не весь автомобиль, а его шасси с кузовом). Иногда криволинейное движение на поворотах дорог автомобилей или поездов условно принимают за поступательное. В подобных случаях говорят, что автомобиль или поезд движутся с такой-то скоростью или с таким-то ускорением.
Примерами криволинейного поступательного движения служат движение вагончика (люльки) подвесной канатной дороги (рис. 7.2, б) или движение спарника (рис. 7.2, в), соединяющего два параллельных кривошипа. В последнем случае каждая точка спарника движется по окружности.
|
|
|
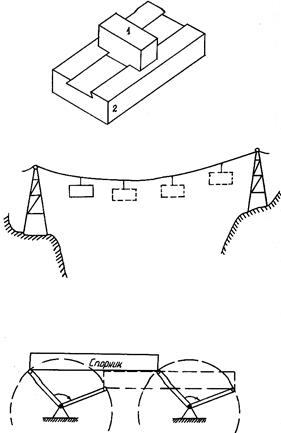
Рис. 7.2. Примеры поступательного движения тел:
а – прямолинейного; б, в – криволинейного
7.2. Вращательное движение.
Угловая скорость, угловое ускорение
Движение твердого тела, при котором все его точки перемещаются по окружности, центры которой расположены на перпендикулярной этим окружностям неподвижной прямой, называется вращательным. Неподвижная прямая, на которой лежат центры круговых траекторий точек тела, называется его осью вращения. Для образования оси вращения достаточно закрепить какие-либо две точки тела. В качестве примеров вращательного движения тел можно привести движение дверей или створок окон при их открывании или закрывании.
Представим себе тело в виде цилиндра, ось AB которого лежит в подшипниках (рис. 7.3).

Рис. 7.3. К анализу вращательного движения твердого тела
Движением одной какой-либо точки однозначно определить вращательное движение тела нельзя.
Для установления закона вращательного движения тела, по которому можно определять его положение в данный момент, проведем через ось вращения тела связанную только с нею неподвижную полуплоскость НП, а внутри тела отметим подвижную полуплоскость, которая вращается около оси вместе с телом, теперь угол φ, образуемый в каждый данный момент времени полуплоскостями НП и ПП, точно определяет положение тела в пространстве (см. рис. 7.3). Угол φ называется углом поворота и выражается в радианах. Чтобы определять положение тела в пространстве в любой момент времени, необходимо знать зависимость между углом поворота φ и временем t, т. е. знать закон вращательного движения тела:
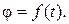
Быстрота изменения угла поворота во времени характеризуется величиной, которая называется угловой скоростью.
Представим, что в некоторый момент времени t положение вращающегося тела определяется углом поворота φ, а в момент t + Δt – углом поворота φ + Δ φ. Следовательно, за время Δt тело повернулось на угол Δ φ, и величина
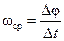
называется средней угловой скоростью.

Единицей угловой скорости является 1 рад/с. Характеристикой быстроты изменения угловой скорости служит угловое ускорение, обозначаемое  . Среднее ускорение
. Среднее ускорение  ;
;
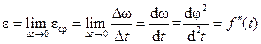 .
.
Единица углового ускорения 1 рад/с2.
Условимся угол поворота, отсчитываемый против хода часовой стрелки, считать положительным, а отсчитываемый по ходу часовой стрелки – отрицательным.
|
|
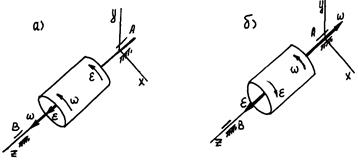
Рис. 7.4. К определению вида вращательного движения
Векторы  и
и  – это скользящие векторы, которые направлены по оси вращения, чтобы, глядя из конца вектора
– это скользящие векторы, которые направлены по оси вращения, чтобы, глядя из конца вектора  (или
(или  ), видеть вращение, происходящее против часовой стрелки.
), видеть вращение, происходящее против часовой стрелки.
Если векторы  и
и  направлены в одну сторону (рис. 7.4, а), то вращательное движение тела ускоренное – угловая скорость возрастает. Если векторы
направлены в одну сторону (рис. 7.4, а), то вращательное движение тела ускоренное – угловая скорость возрастает. Если векторы  и
и  направлены в противоположные стороны, то вращение тела замедленное – угловая скорость уменьшается (рис. 7.4, б).
направлены в противоположные стороны, то вращение тела замедленное – угловая скорость уменьшается (рис. 7.4, б).
7.3. Частные случаи вращательного движения
1. Равномерное вращательное движение. Если угловое ускорение 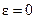 и, следовательно, угловая скорость
и, следовательно, угловая скорость
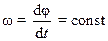 , (7.1)
, (7.1)
то вращательное движение называется равномерным. Из выражения (7.1) после разделения переменных получим

Если при изменении времени от 0 до t угол поворота изменялся от φ0 (начальный угол поворота) до φ, то, интегрируя уравнение в этих пределах:

получаем уравнение равномерного вращательного движения
 ,
,
которое в окончательном виде записывается так:
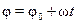 .
.
Если  , то
, то
 .
.
Таким образом, при равномерном вращательном движении угловая скорость
 или при
или при 
 .
.
2. Равнопеременное вращательное движение. Если угловое ускорение
 (7.2)
(7.2)
то вращательное движение называется равнопеременным. Производя разделение переменных в выражении (7.2):

и приняв, что при изменении времени от 0 до t угловая скорость изменилась от  (начальная угловая скорость) до
(начальная угловая скорость) до  , проинтегрируем уравнение в этих пределах:
, проинтегрируем уравнение в этих пределах:
 или
или  ,
,
т. е. получим уравнение
 (7.3)
(7.3)
выражающее значение угловой скорости в любой момент времени.
Закон равнопеременного вращательного движения  или, с учетом уравнения (7.3):
или, с учетом уравнения (7.3):
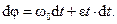
Полагая, что в течение времени от 0 до t угол поворота изменялся от  до
до  , проинтегрируем уравнение в этих пределах:
, проинтегрируем уравнение в этих пределах:
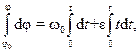 или
или 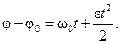
Уравнение равнопеременного вращательного движения в окончательном виде
 (7.4)
(7.4)
Первую вспомогательную формулу получим, исключив из формул (7.3) и (7.4) время:
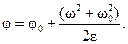 (7.5)
(7.5)
Исключив из тех же формул угловое ускорение  , получим вторую вспомогательную формулу:
, получим вторую вспомогательную формулу:
 (7.6)
(7.6)
где 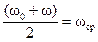 – средняя угловая скорость при равнопеременном вращательном движении.
– средняя угловая скорость при равнопеременном вращательном движении.
Когда  и
и  , формулы (7.3)–(7.6) приобретают более простой вид:
, формулы (7.3)–(7.6) приобретают более простой вид:
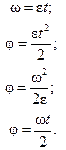
В процессе конструирования угловое перемещение выражают не в радианах, а просто в оборотах.
Угловая скорость, выражаемая количеством оборотов в минуту, называется частотой вращения и обозначается n. Установим зависимость между  (с–1) и n (мин–1). Так как
(с–1) и n (мин–1). Так как  , то при n (мин–1) за t = 1 мин = 60 с угол поворота
, то при n (мин–1) за t = 1 мин = 60 с угол поворота 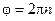 . Следовательно:
. Следовательно:
 .
.
При переходе от угловой скорости  (с–1) к частоте вращения n (мин–1) имеем
(с–1) к частоте вращения n (мин–1) имеем

7.4. Скорости и ускорения различных точек
вращающегося тела
Определим скорость и ускорение любой точки в любой момент времени. Для этой цели установим зависимость между угловыми величинами  ,
,  и
и  , характеризующими вращательное движение тела, и линейными величинами
, характеризующими вращательное движение тела, и линейными величинами 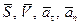 и
и 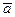 , характеризующими движение точек тела.
, характеризующими движение точек тела.
Допустим, что тело, показанное на рис. 7.5, вращается по закону, описываемому уравнением 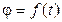 . Требуется определить скорость
. Требуется определить скорость  и ускорение
и ускорение  точки А этого тела, расположенной на расстоянии ρ от оси вращения O. Пусть тело за некоторое время t повернулось на угол φ, а точка А, двигаясь по окружности из некоторого начального положения
точки А этого тела, расположенной на расстоянии ρ от оси вращения O. Пусть тело за некоторое время t повернулось на угол φ, а точка А, двигаясь по окружности из некоторого начального положения  , переместилась на расстояние
, переместилась на расстояние 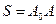 . Так как угол φ выражается в радианах, то
. Так как угол φ выражается в радианах, то
 (7.7)
(7.7)
т. е. расстояние, пройденное точкой вращающегося тела, пропорционально его углу поворота. Расстояние S и угол поворота φ – функции времени, a ρ – величина, постоянная для данной точки. Продифференцируем по времени обе части равенства (7.7) и получим

но 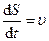 – скорость точки, a
– скорость точки, a 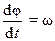 – угловая скорость тела, поэтому
– угловая скорость тела, поэтому
 , (7.8)
, (7.8)
т. е. скорость точки вращающегося тела пропорциональна его угловой скорости.
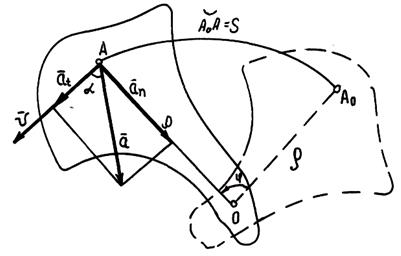
Рис. 7.5. К определению скорости и ускорения точки
Изформулы (7.8) видно, что для точек, расположенных на оси вращения, 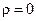 и скорости этих точек также равны нулю. По мере изменения
и скорости этих точек также равны нулю. По мере изменения  , т. е. у точек, находящихся дальше от оси вращения, скорости тем больше, чем больше значение
, т. е. у точек, находящихся дальше от оси вращения, скорости тем больше, чем больше значение  . Пропорциональная зависимость скоростей различных точек вращающегося тела от их расстояний относительно оси вращения показана на рис. 7.6.
. Пропорциональная зависимость скоростей различных точек вращающегося тела от их расстояний относительно оси вращения показана на рис. 7.6.

Рис. 7.6. Распределение скоростей при вращательном движении твердого тела
Продифференцировав обе части равенства (7.8), имеем
 ,
,
но  – касательное ускорение точки, a
– касательное ускорение точки, a  – угловое ускорение тела, значит
– угловое ускорение тела, значит
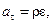 (7.9)
(7.9)
т. е. касательное ускорение точки вращающегося тела пропорционально его угловому ускорению.
Подставив в формулу  значение скорости из формулы (7.8), получим
значение скорости из формулы (7.8), получим
 (7.10)
(7.10)
т. е. нормальное ускорение точки вращающегося тела пропорционально второй степени его угловой скорости.
Из формулы  после подстановки вместо
после подстановки вместо 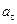 и
и  их значений из формул (7.9) и (7.10) получаем
их значений из формул (7.9) и (7.10) получаем
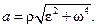 (7.11)
(7.11)
Направление вектора ускорения, т. е. угол  , определяется по одной из формул
, определяется по одной из формул  , причем последнюю из них теперь можно представить в таком виде:
, причем последнюю из них теперь можно представить в таком виде:
 (7.12)
(7.12)
Из формул (7.11) и (7.12) следует, что для точек тела при его вращательном движении по заданному закону можно сначала найти ускорение а, а затем разложить его на касательное ускорение  и нормальное ускорение
и нормальное ускорение  , модуль которых
, модуль которых
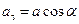 и
и 
7.5. Способы передачи вращательного движения
В технике часто возникает необходимость передачи вращательного движения от одной машины к другой (например, от электродвигателя к станку) или внутри какой-либо машины от одной вращающейся детали к другой. Механические устройства, предназначенные для передачи и преобразования вращательного движения, называются передачами.
Глава 8. Сложное движение
8.1. Сложное движение точки
Примером сложного движения точки может служить:
а) лодка (если ее принять за материальную точку), плывущая от одного берега реки к другому;
б) шагающий по ступенькам движущегося эскалатора метро человек, который также совершает сложное движение относительно неподвижного свода туннеля.
Таким образом, при сложном движении точка, двигаясь относительно некоторой подвижной материальной среды, которую условимся называть подвижной системой отсчета, одновременно передвигается вместе с этой системой отсчета относительно второй системы отсчета, условно принимаемой за неподвижную.
Движение некоторой точки М по отношению к подвижной системе отсчета называется относительным. Движение подвижной системы отсчета вместе со всеми связанными с ней точками материальной среды по отношению к неподвижной системе отсчета для точки М называется переносным. Движение точки М по отношению к неподвижной системе отсчета называется сложным, или абсолютным.
Для того чтобы видеть сложное (абсолютное) движение точки, наблюдатель сам должен быть связан с неподвижной системой отсчета. Если же наблюдатель находится в подвижной системе отсчета, то он видит лишь относительную часть сложного движения.
Представим, что точка М за некоторое время переместилась относительно подвижной системы координат O1X1Y1 из начального положения M0 в положение М1 по траектории M0М1 (траектории относительного движения точки) (рис. 8.1). За это же время Δt подвижная система координат O1X1Y1 вместе со всеми неизменно связанными с ней точками, а значит, и вместе с траекторией относительного движения точки М переместилась в неподвижной системе координат OXY в новое положение:
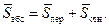

Рис. 8.1. К анализу сложного движения точки
Разделим обе части этого равенства на время движения Δt:
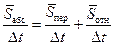
и получим геометрическую сумму средних скоростей:
 ,
,
которые направлены вдоль соответствующих векторов перемещений. Если теперь перейти к пределам при 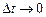 , то получим уравнение
, то получим уравнение
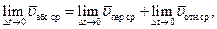

выражающее теорему сложения скоростей: при сложном движении точки абсолютная скорость в каждый момент времени равна геометрической сумме переносной и относительной скоростей.
Если задан угол  , то модуль абсолютной скорости
, то модуль абсолютной скорости
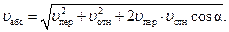
Углы, образуемые векторами абсолютной скорости  с векторами
с векторами 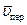 и
и  , определяются по теореме синусов.
, определяются по теореме синусов.
В частном случае при 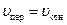 при сложении этих скоростей образуется ромб (рис. 8.2, а) или равнобедренный треугольник (рис. 8.2, б) и, следовательно,
при сложении этих скоростей образуется ромб (рис. 8.2, а) или равнобедренный треугольник (рис. 8.2, б) и, следовательно,


а б
Рис. 8.2. Частный случай
8.2. Плоскопараллельное движение тела
Движение твердого тела, при котором все его точки движутся в плоскостях, параллельных некоторой неподвижной плоскости, называется плоскопараллельным(рис. 8.3).

Рис. 8.3. Плоскопараллельное движение твердого тела
Изучая плоскопараллельное движение тела М, достаточно рассматривать движение его плоского сечения q плоскости ХОY (рис. 8.4).

Рис. 8.4. К анализу плоскопараллельного движения твердого тела
Выберем в сечении q произвольную точку A, которую назовем полюсом. С полюсом А свяжем некоторую прямую KL, а в самом сечении вдоль прямой KL проведем отрезок AB, перемещая плоское сечение из положения q в положение q1. Можно сначала передвинуть его вместе с полюсом А поступательно, а затем повернуть на угол φ.
Плоскопараллельное движение тела – движение сложное и состоит из поступательного движения вместе с полюсом и вращательного движения вокруг полюса.
Закон плоскопараллельного движения можно задать тремя уравнениями:
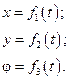
Дифференцируя заданные уравнения плоскопараллельного движения, можно в каждый момент времени определить скорость  и ускорение
и ускорение  полюса, а также угловую скорость
полюса, а также угловую скорость  и угловое ускорение
и угловое ускорение 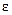 тела.
тела.
Пример 8.1. Пусть движение катящегося колеса диаметром d (рис. 8.5) задано уравнениями

где 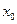 и
и  – м, φ – рад, t – с.
– м, φ – рад, t – с.
Продифференцировав эти уравнения, находим, что скорость полюса O 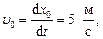 угловая скорость колеса
угловая скорость колеса 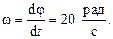 Ускорение полюса и угловое ускорение колеса в данном случае равны нулю. Зная скорость полюса и угловую скорость тела, можно затем определить скорость любой его точки.
Ускорение полюса и угловое ускорение колеса в данном случае равны нулю. Зная скорость полюса и угловую скорость тела, можно затем определить скорость любой его точки.
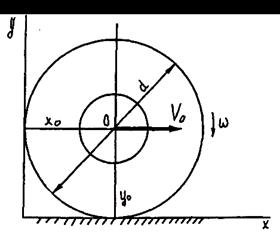
Рис. 8.5. К примеру 8.1
8.3. Определение скорости любой точки тела
при плоскопараллельном движении
Пусть дано плоское сечение q, угловая скорость и скорость полюса которого в некоторый момент времени соответственно  и
и  . Требуется определить скорость какой-либо точки А (рис. 8.6).
. Требуется определить скорость какой-либо точки А (рис. 8.6).
Расчленим плоскопараллельное движение на составные части – поступательную и вращательную. При поступательном движении вместе с полюсом (переносное движение) все точки сечения, и точка А в том числе, имеют переносную скорость  , равную скорости полюса. Одновременно с поступательным сечение q совершает вращательное движение с угловой скоростью
, равную скорости полюса. Одновременно с поступательным сечение q совершает вращательное движение с угловой скоростью  (относительное движение):
(относительное движение):
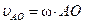 ,
,
где  – относительная скорость точки A (
– относительная скорость точки A ( 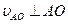 ).
).
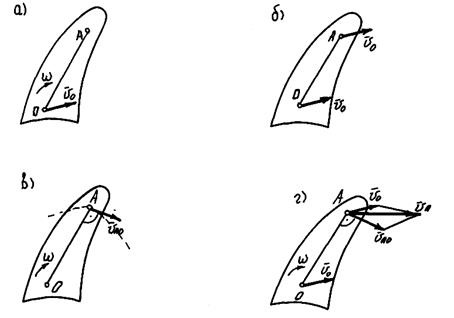
Рис. 8.6. К определению скорости тела при плоскопараллельном движении
Следовательно, в каждый данный момент времени
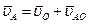 ,
,
т. е. абсолютная скорость точки тела при плоскопараллельном движении равна геометрической сумме скорости полюса и относительной скорости этой точки вокруг полюса.
Модуль абсолютной скорости может быть определен по формуле
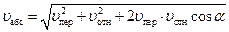 ,
,
а направление – с помощью теоремы синусов. Если же направление абсолютной скорости известно, то ее модуль проще определить на основании следующей теоремы: проекции скоростей двух точек твердого тела на прямую, соединяющую эти точки, равны между собой.
Допустим, что известны скорости  и
и 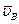 точек A и В какого-либо тела (рис. 8.7). Приняв за полюс точку A, получим
точек A и В какого-либо тела (рис. 8.7). Приняв за полюс точку A, получим
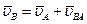 .
.
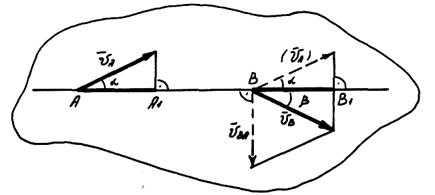
Рис. 8.7. Векторы скоростей точек плоской фигуры
Относительная скорость  перпендикулярна АВ. Следовательно,
перпендикулярна АВ. Следовательно,  или
или  . Теорема доказана.
. Теорема доказана.
Глава 9. Движение несвободной
материальной точки
9.1. Основные понятия и аксиомы динамики
Динамика изучает движение материальных тел под действием сил. В основе динамики лежат следующие аксиомы.
Аксиома 1 (принцип инерции). Всякая изолированная материальная точка находится в состоянии покоя или равномерного и прямолинейного движения, пока приложенные силы не выведут ее из этого состояния.
Аксиома 2 (основной закон динамики). Ускорение материальной точки пропорционально действующей силе F и направлено по той прямой, по которой действует эта сила (рис. 9.1).
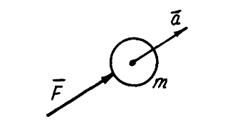
Рис. 9.1. К основному закону динамики
Математически вторая аксиома записывается векторным равенством
 ,
,
где m – коэффициент пропорциональности, выражающий меру инертности материальной точки и называемый ее массой.
В Международной системе единиц (СИ) масса выражается в килограммах.
Зависимость между числовыми значениями (модулями) сил и ускорения выражается равенством
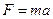 .
.
На все материальные тела вблизи Земли действует сила тяжести G. При свободном падении на Землю телá любой массы приобретают одно и то же ускорение g, которое называется ускорением свободного падения. Для свободно падающего тела из предыдущего уравнения следует зависимость:
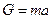 .
.
Таким образом, значение силы тяжести тела в ньютонах равно произведению его массы на ускорение свободного падения.
Аксиома 3 (закон независимости действия сил). Если к материальной точке приложена система сил, то каждая из сил системы сообщает точке такое же ускорение, какое она сообщила бы, действуя одна.
Таким образом, при одновременном действии на материальную точку массой m, например, четырех сил, ускорение а, полученное точкой, можно определить геометрически сложив ускорения  и
и  , возникающие под действием каждой силы в отдельности (рис. 9.2). В то же время ускорение
, возникающие под действием каждой силы в отдельности (рис. 9.2). В то же время ускорение  пропорционально равнодействующей
пропорционально равнодействующей 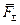 тех же сил:
тех же сил:

где  и
и  .
.

Рис. 9.2. К закону независимости действия сил
Аксиома 4. Две материальные точки действуют друг на друга с силами, равными по модулю и направленными в противоположные стороны.
9.2. Свободная и несвободная точки
Материальная точка, движение которой в пространстве не ограничено какими-либо связями, называется свободной. Примером свободной материальной точки может служить искусственный спутник Земли в околоземном пространстве или летящий самолет. Их перемещение в пространстве ничем не ограничено, поэтому летчик на спортивном самолете способен проделывать различные сложные фигуры высшего пилотажа.
Задачи динамики сводятся к двум основным:
1) задается закон движения точки, требуется определить действующую на нее силу или систему сил (первая задача динамики);
2) задается система сил, действующая на точку, требуется определить закон движения (вторая задача динамики).
Обе задачи динамики решаются с помощью основного закона динамики, записанного в форме 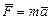 или
или  .
.
Материальная точка, свобода перемещения которой ограничена наложенными связями, называется несвободной. Примером несвободной материальной точки может служить движущийся по рельсам трамвай, если пренебречь его формой и размерами. Для несвободной материальной точки все внешние силы необходимо делить на две категории: активные (движущие) силы и реакции связи (пассивные силы). В связи с этим первая задача динамики несвободной точки сводится к определению реакций связей, если заданы законы движения точки и действующие на нее активные силы. Вторая задача динамики сводится к тому, чтобы, зная действующие на точку активные силы, определить, во-первых, закон движения точки и, во-вторых, реакции связей.
Если несвободную материальную точку освободить от связей и заменить связи их реакциями, то движение точки можно рассматривать как свободное, а основному закону динамики придать такой вид:
 ,
,
где 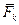 – активные силы;
– активные силы;
 – реакции связей;
– реакции связей;
m – масса точки;
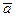 – ускорение точки, полученное в результате действия внешних сил (активных и пассивных).
– ускорение точки, полученное в результате действия внешних сил (активных и пассивных).
9.3. Силы инерции
Сила, численно равная произведению массы материальной точки на приобретенное ею ускорение и направленная в сторону, противоположную ускорению, называется силой инерции(рис. 9.3):
 .
.

Рис. 9.3. Сила инерции
Сила инерции в действительности не приложена к получившей ускорение материальной точке, а действует на точку или тело, которое сообщает ускорение этой точке.
Поясним это несколькими примерами.
Тяжелый груз, масса которого m, висит на непрочной, но способной выдержать натяжение R = G нити (рис. 9.4, а). Если теперь резко потянуть нить вертикально вверх, то она может оборваться (рис. 9.4, б). На нить начинает действовать дополнительная сила инерции 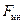 , численно равная
, численно равная  , противодействующая выходу груза из состояния инерции (рис. 9.4, в). Нить может оборваться и в том случае, если толкнуть в горизонтальном направлении подвешенный груз, заставив его раскачиваться на нити (рис. 9.4, г).
, противодействующая выходу груза из состояния инерции (рис. 9.4, в). Нить может оборваться и в том случае, если толкнуть в горизонтальном направлении подвешенный груз, заставив его раскачиваться на нити (рис. 9.4, г).
При криволинейном движении материальной точки (рис. 9.5) у нее возникает ускорение 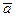 , которое обычно заменяют двумя составляющими ускорениями:
, которое обычно заменяют двумя составляющими ускорениями:  (нормальное ускорение) и
(нормальное ускорение) и  (касательное ускорение). Поэтому при криволинейном движении материальной точки возникают две составляющие силы инерции
(касательное ускорение). Поэтому при криволинейном движении материальной точки возникают две составляющие силы инерции 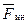 : нормальная (иначе центробежная) сила инерции
: нормальная (иначе центробежная) сила инерции
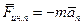
и касательная (иначе тангенциальная) сила инерции


а б в г
Рис. 9.4. К анализу дейсвия сил инерции

Рис. 9.5. Векторы ускорений и сил инерции
9.4. Принцип Даламбера
Силы инерции широко используются при расчетах и решении технических задач, причем использование сил инерции позволяет решения многих задач, в которых рассматривается движение несвободной материальной точки, свести к знакомым нам уравнениям статики:

Условно прикладывая силу инерции  к движущейся материальной точке, можем считать, что активные силы
к движущейся материальной точке, можем считать, что активные силы 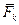 , реакции связей
, реакции связей  и сила инерции
и сила инерции  образуют уравновешенную систему (принцип Даламбера).
образуют уравновешенную систему (принцип Даламбера).
Решение задач динамики с помощью принципа Даламбера иногда называют методом кинетостатики.
Глава 10. Работа и мощность
Дата добавления: 2015-06-17; просмотров: 1717;
