Потенциальная энергия частицы в силовом поле.

То обстоятельство, что работа консервативной силы (для стационарного поля) зависит только от начального и конечного положений частицы в поле, позволяет ввести важное физическое понятие потенциальной энергии (функции состояния). Возьмем стационарное поле консервативных сил, например электростатическое поле в котором мы перемещаем частицу (заряд) из разных точек 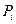в некоторой фиксированной точке О (точка отсчета). Найдем работу сил поля. Поскольку работа сил поля не зависит от пути, то остаётся зависимость её только от положения т. 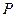(О— фиксировано) т.е. от предела интегрирования

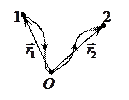
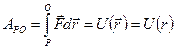Это значит, что данная работа будет некоторой функцией радиус-вектора 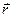точки . Функцию 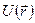называют потенциальной энергией частицы в поле сил. Теперь найдем работу при перемещении частицы из т.1 в т.2. Т.к. она не зависит от формы пути: то 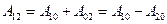или с учетом (*)

;

;

(**)

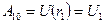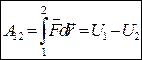Правая часть представляет убыль потенциальной энергии, т.е. разность начальную и конечную значений потенциальной энергии. ( 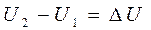— приращение); ( 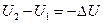— убыль). Т.о. работа сил Оля на пути 1—2 равна убыли потенциальной энергии. Так как работа сил поля определяется лишь разностью энергий в двух точек, а не их абсолютного значения, то частица в т.О можно приписать любое, наперед выбранное значение потенциальной энергии.

Однако, как только зафиксирована потенциальная энергия в одной, какой-либо точке, значения её во всех остальных точках поля определяется однозначно выражением (**). Эта формула позволяет найти вид 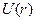для любого стационарного поля консервативных сил. Для этого достаточно вычислить работу совершаемую силами поля между двумя любыми точками и представить её в виде убыли некоторой функции 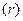, которая и есть потенциальной энергией. Так и было ране сделано при вычислении работы гравитационной, упругой и силы тяжести. Отсюда видно, что потенциальная энергия частицы в данных полях имеет вид

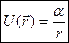— гравитационная, кулоновская +С – постоянная.

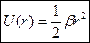— упругой +С

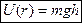— в поле тяжести.

Отметим еще раз, что потенциальная энергия определяется с точностью до некоторой постоянной величины, что несущественно, т.к. во всех формулах входит разность её значения в двух положениях частицы, поэтому постоянная выпадает, и её опускают. Кроме этого важно заметить, что потенциальную энергию следует относить не к частице в поле а к системе взаимодействующих частиц и тела, создающего поле. При данном характере взаимодействия потенциальная энергия зависит только от положения частицы относительно этого тела.