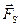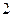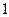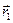Энергия и робота
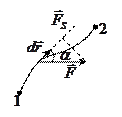 Пусть частица под действием силы
Пусть частица под действием силы 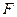 совершает перемещение по некоторой траектории 1-2. в общем случае сила
совершает перемещение по некоторой траектории 1-2. в общем случае сила 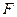 может меняться во времени по модулю, например, но не элементарном перемещении
может меняться во времени по модулю, например, но не элементарном перемещении 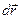 её можно считать
её можно считать 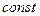 .
.
Действие силы на перемещении 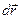 характеризуется физической величиной, равной скалярному произведению
характеризуется физической величиной, равной скалярному произведению 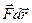 , которое называется элементарной работой силы
, которое называется элементарной работой силы 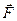 на перемещении
на перемещении 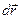 . Её можно ещё записать как
. Её можно ещё записать как 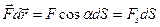 , где
, где 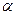 — угол между
— угол между 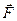 и
и 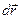
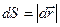 - элементарный путь
- элементарный путь 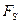 проекция вектора
проекция вектора 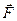 на вектор
на вектор 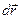
|
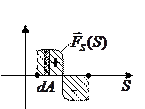 Значит элементарная работа
Значит элементарная работа 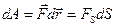 (*)
(*)
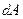 - величина алг. она и
- величина алг. она и 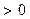 и
и 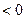 и = 0 при
и = 0 при 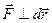 .
.
Суммируя ( интегрируя ) по всем элементарным участкам пути от 1 к 2 найдем работу силы 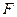 на данном пути.
на данном пути.
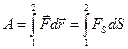 .
.
Геометрический смысл этого выражения виден из рисунка 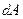 — полоска;
— полоска; 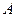 — площадь под прямой. Над осью работа положительна, под — отрицательна.
— площадь под прямой. Над осью работа положительна, под — отрицательна.
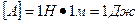 .
.
Найдем для примера работу некоторых центральных сил.
1. 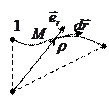
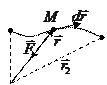
|
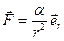 ;
; 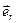 —орт радиус вектора
—орт радиус вектора 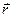 . Элементарная работа не ????
. Элементарная работа не ???? 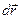 :
: 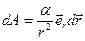 ;
; 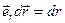 — приращение модуля вектора
— приращение модуля вектора 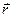 ;
; 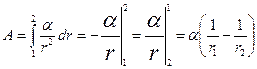 .
.
2. 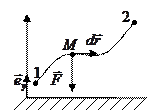
|
|
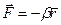 ;
; 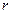 — радиус вектор частицы М относительно точки О. элементарная работа
— радиус вектор частицы М относительно точки О. элементарная работа 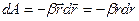 ;
; 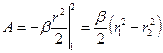 .
.
3. Работа сил тяжести. 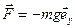 ;
; 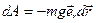 ;
; 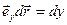 — приращение координаты
— приращение координаты 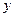 .
.
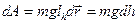
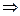
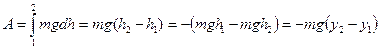
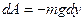 ;
; 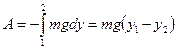 .
.
Работа всех этих сил не зависит от формы пути а только от положения точек 1,2. Эта особенность не всех сил. Силы трения не обладают таким свойством.
3.2 Мощность по определению это работа, выполненная за единицу времени. Если за промежуток времени 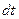 сила
сила 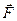 совершает работу
совершает работу 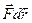 , то мощность, развиваемая этой силой в данный момент времени
, то мощность, развиваемая этой силой в данный момент времени 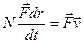 т.е. скалярное произведение
т.е. скалярное произведение 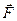 и
и 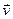 .
.
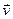 — скорость движения точки приложения силы.
— скорость движения точки приложения силы.
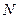 — как и работа величина алгебраическая.
— как и работа величина алгебраическая.
Зная 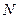 можно найти работу, которая совершает сила
можно найти работу, которая совершает сила 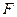 за время
за время 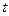
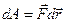
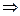
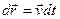
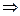
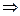
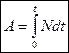
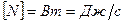 .
.
Дата добавления: 2015-06-17; просмотров: 761;