Связь между потенциальной энергией и силой для консервативного поля.
Взаимодействие частицы с окружающими телами можно описать либо с помощью сил либо с помощью потенциальной энергией. Первый способ более общий , т.к. он применим и к силам, для которых нельзя ввести понятие потенциальной энергии (силы трения). Второй способ удобен тем, что существует связь между потенциальной энергией и силой со стороны поля. Зная эту связь, можно по виду зависимости 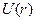 — функции положения частицы в поле, находить поле сил
— функции положения частицы в поле, находить поле сил 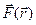 .
.
Найдем эту связь. Известно, что работа консервативных сил при перемещении частицы из одной точки статического поля в другую может быть представлена в виде убыли потенциальной энергии частицы 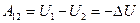 . Это можно записать и для элементарного перемещения
. Это можно записать и для элементарного перемещения 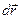 .
.
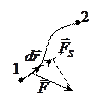
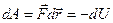
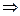
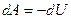 т.к.
т.к. 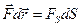 ;
; 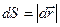 — элементарный путь или
— элементарный путь или 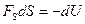 ;
; 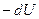 — убыль потенциальной энергии в направлении перемещения
— убыль потенциальной энергии в направлении перемещения 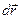 ; отсюда:
; отсюда: 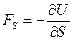 т.е. проекция силы поля
т.е. проекция силы поля 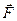 в данной точке на направление перемещения
в данной точке на направление перемещения 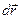 равна убыли потенциальной энергии в этом направлении. Символ
равна убыли потенциальной энергии в этом направлении. Символ 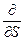 указывает, что произведение берется по определенному направлению. Перемещение
указывает, что произведение берется по определенному направлению. Перемещение 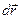 можно брать в любом направлении, например вдоль осей
можно брать в любом направлении, например вдоль осей 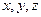 . Если вдоль
. Если вдоль 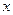 то
то 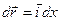 ; а
; а 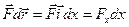 ,
, 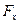 — проекция силы
— проекция силы 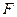 на орт
на орт 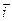 (а не на перемещение
(а не на перемещение 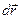 , как в случае
, как в случае 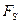 ). Т.о. относительно оси
). Т.о. относительно оси 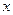 можно записать
можно записать 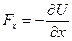 . Символ
. Символ 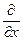 означает, что
означает, что 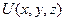 при дифференцировании должна расти как функция одного аргумента
при дифференцировании должна расти как функция одного аргумента 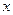 , а остальные аргументы —
, а остальные аргументы — 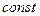 . Значит
. Значит 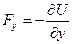 ;
; 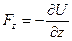 . Зная проекции
. Зная проекции 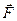 можно найти и сам вектор
можно найти и сам вектор 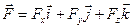 или
или 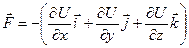 . Скобка называется градиент скалярной функции
. Скобка называется градиент скалярной функции 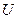 , и обозначается
, и обозначается 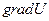 или
или 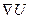 т.о.
т.о. 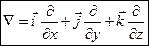 — символический вектор или оператор Гамильтона.
— символический вектор или оператор Гамильтона. 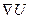 — формально можно рассматривать как произведение символического вектора
— формально можно рассматривать как произведение символического вектора 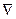 на скаляр
на скаляр 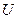 т.е. сила действующая со стороны поля на частицу равна со знаком минус градиент потенциальной энергии частицы в данной тоске поля. Т.о. зная
т.е. сила действующая со стороны поля на частицу равна со знаком минус градиент потенциальной энергии частицы в данной тоске поля. Т.о. зная 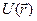 можно найти
можно найти 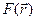 .
.
Дата добавления: 2015-06-17; просмотров: 1098;
