РЕЗОНАНС НАПРЯЖЕНИЙ

Явление совпадения по фазе напряжения и тока в R, L, C -цепи называется электрическим резонансом.

В цепях переменного тока с последовательным соединением R, L, C - элементов при равенстве 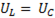возникает резонанс напряжений.

При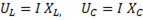

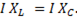
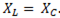
т.е. резонанс напряжений наступает при равенстве реактивных сопротивлений.

Условием резонанса напряжений является равенство

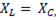(6-43)

или

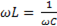(6-44)

Поэтому в цепи переменного тока резонанс напряжений может наступить:

1) если при постоянных L и C частота сигнала, подаваемого в цепь, изменяясь, становится равной ν = = ; ( )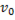

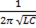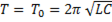2) если при постоянной частоте входного сигнала и постоянной индуктивности емкость конденсатора меняется и становится равной: С = ;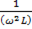

3) если при постоянной частоте входного сигнала и постоянной емкости меняется индуктивность и становится равной: L = ;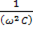

4) если при постоянной частоте входного сигнала изменение обеих величин L и C приводит к равенству: .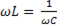

Таким образом, чтобы в цепи наступил резонанс напряжений, необходимо обеспечить определенное соотношение между величинами ν, L, C, т.е. резонанса в цепи можно добиться путем регулирования (подбора) параметров индуктивного и емкостного элементов, а также с помощью изменения частоты питающего тока. При резонансе частота тока (напряжения) равна частоте собственных колебаний цепи (контура).

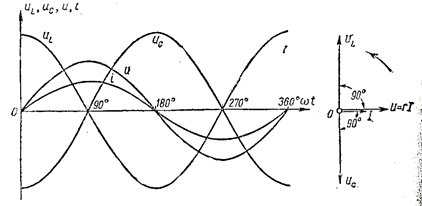
Рис. 77 Графики и векторная диаграмма для резонанса напряжений.

При резонансе напряжений выражение

U = 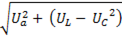= 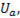(6-45)

так как .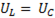

Полное сопротивление цепи

Z = 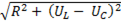= R, (6-46)

так как = .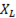

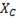Полная мощность цепи

S = 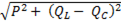= P, (6-47)

так как .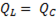

Фазовый сдвиг между током и напряжением

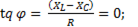(6-48)

так как 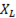= 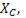следовательно .

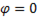Коэффициент мощности

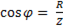= 1, (6-49)

так как Z =R

Таким образом, электрическая цепь переменного тока в режиме резонанса представляет собой чисто активную нагрузку.

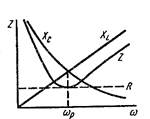
Зависимость параметров цепи от частоты. Практический интерес представляют соотношения между параметрами цепи и их зависимость от частоты тока. На рис.78 а показаны

а б

Рис.78

кривые 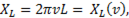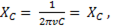R = R(v). Т.к. активное сопротивление практически от частоты не зависит то график R = R(v) представляет прямую параллельную оси абсцисс. Индуктивное сопротивление 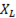прямо пропорционально, а емкостное сопротивление 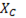обратно пропорционально частоте тока.

До резонанса 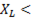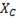, при резонансе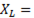 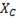, после резонанса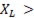 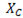. При резонансе полное реактивное сопротивление

=

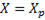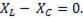
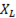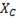Полное сопротивление цепи Z, также зависит от частоты. До и после резонанса оно растет за счет увеличения или . При резонансе Z = R.

По закону Ома ток в последовательной R, L, C – цепи

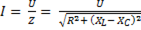. (6-50)

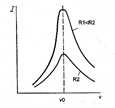
При резонансе (X_L =X_C) и ток равен максимальному значению, в то время как до (X_L < X_C) и после (X_L > X_C) резонанса он уменьшается. При v=0, X_C = ∞, I = 0. Аналогично при v =∞, X_L =∞, I = 0. На рис. б показаны графики I (v).

Кривая зависимости тока от частоты называется резонансной кривой. По характеру изменения тока в R, L, C – цепи легко установить состояние резонанса в ней – максимальное значение тока в цепи указывает на момент резонанса.

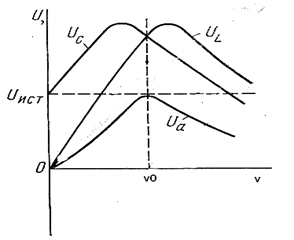
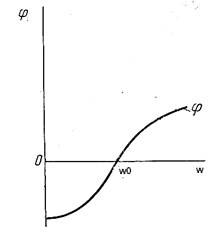
Рис. 79 Рис.80

Напряжение на резистивном элементе изменяется пропорционально току: 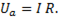При резонансе, когда ток максимален, напряжение U_a также максимально и равно напряжению источника питания U_ист (рис. ). При ω = 0; ∞ ток I = 0; U_a = 0. На рис.79а изображена зависимость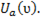

Напряжение на индуктивном элементе 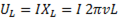пропорционально току I и частоте . .

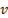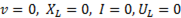При увеличении частоты напряжение на индуктивном элементе растет и при частоте, близкой к резонансной, достигает максимального значения; по мере дальнейшего увеличения частоты ток, а следовательно, и индуктивное напряжение уменьшаются. При 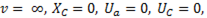поэтому индуктивное напряжение равно напряжению источника питания. Кривая 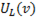изображена на рис. 79а .

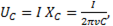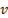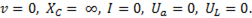Напряжение на емкостном элементе следовательно, оно пропорционально току I и обратно пропорционально частоте . При Поэтому емкостное напряжение компенсирует приложенное напряжение к цепи, т.е. 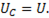При увеличении частоты напряжение 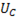растет и при частоте, близкой к резонансной, достигает максимального значения; по мере дальнейшего увеличения частоты ток и емкостное напряжение уменьшаются. При 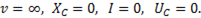Кривая 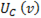изображена на рис. .

Сдвиг фаз определяется из выражения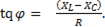

При 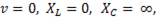т.е. 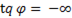, что соответствует .

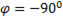При 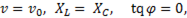что соответствует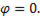

При 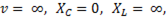т.е. 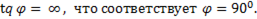График зависимости 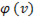изображен на рис. 80 .

7. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ R, L, C – ЭЛЕМЕНТОВ

В цепь переменного тока параллельно включены реальная катушка индуктивности и конденсатор с потерями (рис. 81 ). Эту цепь можно представить как цепь с двумя ветвями, в одной из которых включены элементы R₁ и L₁ , а в другой элементы R₂ и C₂ (рис. 81а). Ветви электрической цепи находятся под одинаковым напряжением

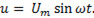(6-51)

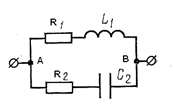
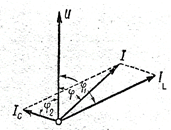
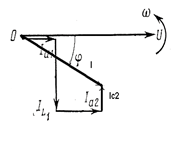
а б в

Рис. 81 Параллельное соединение R, L, C – элементов: а –схема, б.в – векторные диаграммы токов.

Первая ветвь содержит активное сопротивление и индуктивность, следовательно, ток отстает от напряжения на угол 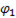, т.е

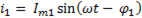. (6-52)

Причем,

,

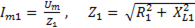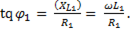
Характер второй ветви активно – емкостной, следовательно, ток опережает напряжение на угол 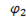и

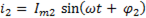. (6-53)

Причем,

,

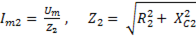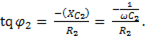
Полный или результирующий ток

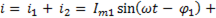
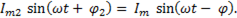(6-54)

При сложении получается синусоидальная величина с той же частотой и начальной фазой φ. Для нахождения 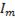и воспользуемся правилом векторного сложения .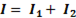

Построение векторной диаграммы начинаем с ориентации на плоскости вектора U (рис. 81б,в). Под углом φ₁ к напряжению откладывается вектор амплитудного ( с учетом знака), либо действующего значения тока I₁ в первой ветви, а под углом φ₂ вектор тока I₂ во второй ветви ( с учетом знака). Суммируем вектора 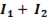( правило параллелограмма) и получаем вектор результирующего тока 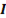.Модуль этого вектора определяем по теореме косинусов

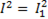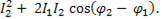+ (6-55)

Можно поступить иначе и от косого треугольника токов перейти к прямоугольному треугольнику.

Спроектируем вектора токов на вектор напряжения, получим активную составляющую тока:

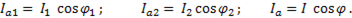(6-56)

Cоставляющие, направленные по линии, перпендикулярной линии напряжения, называют реактивными:

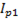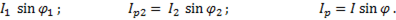= (6-57)

Составляющие результирующего тока могут быть определены как

Т.е. равны сумме составляющих отдельных ветвей. При этом необходимо учитывать их знак. Для ветви с индуктивным элементом реактивную составляющую тока берут со знаком плюс, для ветви с емкостным элементом – со знаком минус.

Из треугольника токов находим

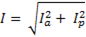. (6-58)

Электрическая проводимость. Каждый элемент цепи может характеризоваться сопротивлением или проводимостью. Разделим все стороны треугольников токов (рис. 81в ) на напряжение. Получим треугольник проводимостей, где каждая из сторон представляет соответствующую проводимость.

Отношение активного тока к напряжению – активная проводимость q :

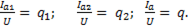(6-59)

Отношение реактивного тока к напряжению – реактивная проводимость b:

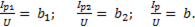(6-60)

Отношение результирующего тока к напряжению – полная проводимость y:

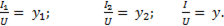(6-61)

Единица измерения проводимости –сименс (См=1/ом).

Из диаграммы видно, что составляющие полной проводимости могут быть определены как

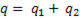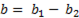; ; (6-62)

Тогда полная проводимость

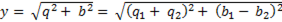. (6-63)

Аналогично для каждой отдельной ветви можно записать

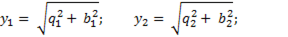
Воспользовавшись диаграммой можно записать

= = =

= = =

= = =

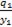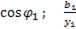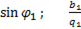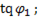
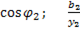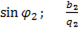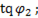
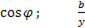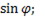
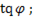
Связь между сопротивлением и проводимостью. Часто при решении практических задач исходными данными являются сопротивления отдельных элементов цепи, а необходимо определить проводимости и сопротивления всей цепи.

Известно, что 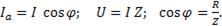Если эти значения подставить в ( ), то

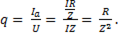(6-64)

Аналогично 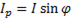; 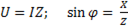. Подставляя эти выражения в ( ), получим

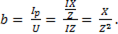(6-65)

Реактивные проводимости сохраняют знак соответствующего сопротивления, т.е.

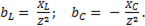(6-66)

Полную проводимость можно получить из ( )

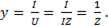(6-67)

Таким образом, полная проводимость цепи равна обратной величине полного сопротивления.

Электрическая мощность. Диаграмму мощностей можно получить из диаграммы токов. Для этого необходимо модули токов умножить на напряжение U:

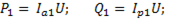(6-68)

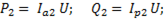
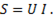(6-69)

Из диаграммы мощностей следует

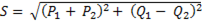. (6-70)

Таким образом, при любом числе элементов, включенных параллельно, результирующие ток, проводимость, мощность записываются как корень квадратный из суммы квадратов арифметических сумм активных и алгебраических сумм реактивных значений соответствующих параметров.