ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ С ИНДУКТИВНОСТЬЮ
Рассмотрим идеальную катушку индуктивности, для которой Rk =C = 0 (Rk – активное сопротивление катушки, С – межвитковая емкость). L – индуктивность катушки. Пусть напряжение u = Um 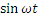 . По цепи протекает переменный ток. Так как ток в цепи изменяется, следовательно в катушке индуцируется эдс индукции eL = -L di/dt. Уравнение электрического
. По цепи протекает переменный ток. Так как ток в цепи изменяется, следовательно в катушке индуцируется эдс индукции eL = -L di/dt. Уравнение электрического
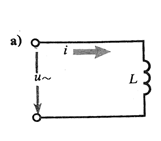
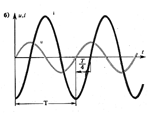
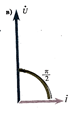
Рис. 69 Цепь переменного тока с индуктивным элементом: а – схема, б.в – временная и векторная диаграммы.
состояния имеет вид
u + eL = I Rk = 0. (6-10)
Откуда следует, что u = - eL = L di/dt.
Из уравнения следует, что для любого момента времени (u) численно равна (eL) и эти величины находятся в противофазе.
di = u/L dt = Um 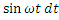 . (6-11)
. (6-11)
Проинтегрируем последнее выражение 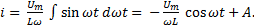
А – постоянная интегрирования, которая при отсутствии постоянной составляющей тока равна нулю.
Заменим - 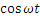 =
= 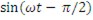 .
.
Тогда мгновенное значение тока приобретает вид:
i = Um/ωL sin(𝜔𝑡− 𝜋/2).
Обозначим Um/ωL = Im.
В окончательном виде выражение для тока в цепи с индуктивным элементом
i = Im 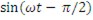 . (6-12)
. (6-12)
Из сравнения аналитических уравнений напряжения и тока следует, что в результате возникновения в цепи эдс индукции между этими характеристиками возникает фазовый сдвиг равный π/2 или напряжение опережает ток на угол π/2. Это означает, что с нарастанием напряжения от нуля до максимума ток падает по абсолютной величине от максимума до нуля и наоборот (рис. б).
На векторной диаграмме (рис. в), если вектор тока располагается горизонтально, то вектор напряжения – с опережением по фазе на угол π/2.
Индуктивное сопротивление. Произведение 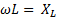 - называется индуктивным сопротивлением, которое пропорционально частоте тока (ω =2πν) и индуктивности элемента цепи.
- называется индуктивным сопротивлением, которое пропорционально частоте тока (ω =2πν) и индуктивности элемента цепи.
Измеряется индуктивное сопротивление в омах (Ом).
Таким образом, любой элемент цепи, обладающий индуктивностью, создает определенное сопротивление при прохождении через него переменного тока. Это можно пояснить тем, что в индуктивном элементе при прохождении переменного тока происходит возбуждение эдс индукции eL, которая согласно правила Ленца своим действием направлена против причины, ее порождающей, следовательно, она создает препятствие на пути движения тока. Хотя индуктивное и активное сопротивления имеют одинаковые размерности, причины, их порождающие, различны.
Индуктивное сопротивление – это сопротивление, которое оказывает току индуктированная эдс, возникающая в этом элементе при прохождении через него переменного тока.
Для постоянного тока ν=0 и, следовательно, 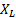 =0. Для переменного тока, с изменяющейся
=0. Для переменного тока, с изменяющейся
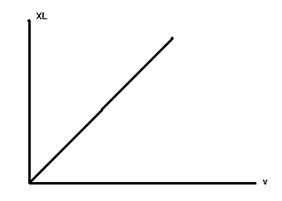
Рис. 70 Частотная зависимость индуктивного сопротивления.
частотой от нуля до бесконечности величина 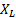 увеличивается по линейному закону от
увеличивается по линейному закону от 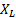 = 0 до
= 0 до 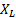 = ∞ (рис. )
= ∞ (рис. )
Уравнение мощности. В цепи с индуктивным элементом мгновенное значение мощности
p = ui = Im ,sin-(𝜔𝑡− 𝜋/2). Um 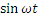 = - Im
= - Im 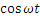 Um ,sin-𝜔𝑡. (6-13)
Um ,sin-𝜔𝑡. (6-13)
Заменим 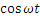
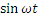 =
= 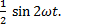
Получим p = - UmIm/2 ∙ 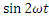 = - UI
= - UI 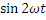 . (6-14)
. (6-14)
Это выражение показывает, что кривая мощности изменяется по закону синуса, но с двойной частотой 2ω.
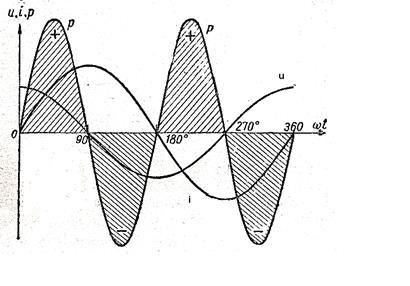
Рис. 71 Кривые мгновенных значений напряжения, тока и мощности для цепи, содержащей индуктивность.
Когда u и i имеют одинаковые знаки (рис.71 ), то кривая р положительна и располагается выше оси абсцисс. Если же u и i имеют разные знаки, то кривая р отрицательна и располагается ниже оси абсцисс.
В первую четверть периода ток, а вместе с ним и магнитный поток катушки увеличивается. Катушка забирает от источника энергии мощность. В это время энергия забираемая от источника идет на создание магнитного поля (мощность положительна). Количество энергии, запасаемое в магнитном поле за время роста тока, можно определить как :
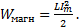 (6-15)
(6-15)
За вторую четверть периода ток убывает. ЭДС индукции, которая в первую четверть периода стремилась помешать возрастанию тока, теперь, когда ток начинает убывать, будет мешать ему уменьшаться. Сама катушка становится как бы генератором электрической энергии. Она возвращает источнику энергию, запасенную в ее магнитном поле. Мощность отрицательна и кривая р располагается ниже оси абсцисс.
За вторую половину периода явление повторяется. Таким образом, между источником переменного напряжения и катушкой, содержащей индуктивность, происходит обмен мощностью. В течение первой и третьей четвертей периода мощность поглощается катушкой, в течение второй и четвертой четвертей мощность, в равной степени, возвращается источнику.
В этом случае, в среднем, расхода мощности не будет, несмотря на то, что на зажимах цепи есть напряжение U и в цепи протекает ток I.
Вычислим активную мощность за время равное периоду
P = 1/T 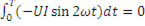
(интеграл от синусоидальной функции в пределах двух периодов равен нулю).
Тот же результат мы получим, если вычислим активную мощность по формуле
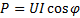 . (6-16)
. (6-16)
Так как между напряжением и током существует фазовый сдвиг равный 900 и 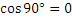 .
.
Поэтому активная мощность также равна нулю, т.е. расхода мощности нет.
Реактивная (индуктивная) мощность количественно оценивается амплитудой кривой мощности:
QL = U I 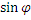 = I2 XL. (6-17)
= I2 XL. (6-17)
и измеряется - вольт-ампер реактивный (вар).
Дата добавления: 2015-06-17; просмотров: 4228;
