Принципы построения систем подчиненного регулирования в электроприводах
Применение одной обратной связи в электроприводе не дает высоких статических и динамических показателей. Улучшение характеристик электроприводов привело к тому, что начали появляться электроприводы с несколькими обратными связями с наличием нескольких контуров, количество которых соответствовало количеству контролируемых параметров, таких как ток, напряжения якоря, скорость вращения двигателя, положения вала приводимого механизма и др. Электропривод с двумя обратными связями по току и скорости изображен на (рис.1.19). На входе регулятора каждого из контуров сравниваются сигналы, пропорциональные заданному и действительному значениям выходной величины данного контура, а выходное напряжение регулятора служит сдающим сигналом для последующего контура. Системы, построенные по такому принципу, называют системами подчиненного регулирования.

(а)

(б)
Рис.1.19. Электропривод с обратными связями по току и скорости
На рис.1.19 каждый контур системы регулирования электропривода имеет регуляторы скорости, тока wрс, wрт и объекты регулирования wр1,wр2. Каждый внутренний контур регулирования подлежит оптимизации, т. е. такому выбору параметров регулятора, при котором удовлетворяется заданное качество регулирования.
Регулятор любого контура представляет собой в большинстве случаев последовательное корректирующее звено. Передаточная функция регулятора определяется структурой и параметрами соответствующего звена объекта регулирования, а также критерием оптимизации этого контура. Каждый внутренний контур регулирования подлежит оптимизации, т. е. такому выбору параметров регулятора, при котором удовлетворяется заданное качество регулирования. Под заданным качеством регулирования понимается переходной процесс при ступенчатом входном сигнале, характеризующий определенную перерегулированием и быстродействием. Наибольшее распространение получили два критерия оптимизации: модульный и симметричный. 
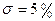
При модульном критерии оптимизации отработка ступенчатого входного сигнала происходит с перерегулирование 4.3% (рис.1.20(а)). Передаточная функция замкнутого контура с регулятором приводится к виду колебательного звена с коэффициентом демпфирования 
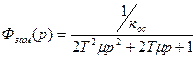 , (1.40)
, (1.40)
где Тµ - малая некомпенсированная постоянная времени в контуре;
кос – коэффициент передачи обратной связи.
Длительность переходного процесса равна 4.7 Тµ и не зависит от постоянной времени объекта регулирования. Такой способ настройки называется еще настройкой на оптиум по модулю (ОМ). Смысл этого термина в том, что при настройке на ОМ стремится в широкой полосе частот сделать модуль частотной характеристики замкнутого контура к единице.
Симметричный критерий оптимизации (СО) широко применяется в контурах, содержащих два интегральных звена или одно интегральное и одно инерционное звено в объекта регулирования при достаточно большой постоянной времени объекта регулирования.
Передаточная функция замкнутого контура по управляемому воздействию имеет вид: 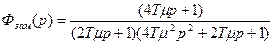 , (1.41)
, (1.41)
При ступенчатом управляющем воздействии время первого достижения выходной величины установившегося значения в контуре, настроенном на СО, составляет 3.1 с Тµ, максимальное перерегулирование достигает 43% (рис.1.20(б)).
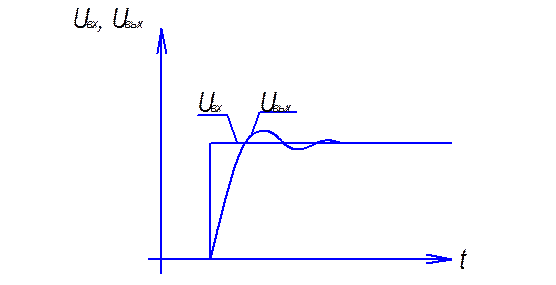
(а) Настройка на модульный оптиум.
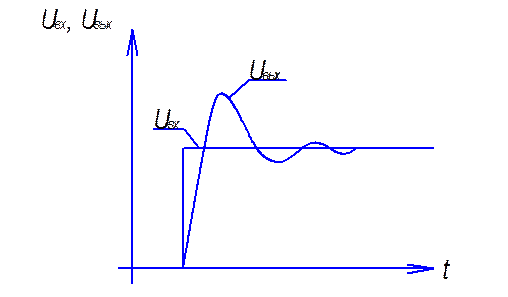 (б) Настройка на симметричный оптиум.
(б) Настройка на симметричный оптиум.
Рис.1.20 (а),(в) Критери оптимизации.
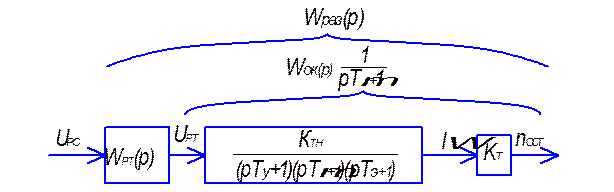
Проведем синтез двухконтурной системы электропривода с подчиненным регулированием. Оптимизация начинается с внутреннего токового контура по модульному критерию, структурная схема которого приведена на (рис.1.21(а)). На структурной схеме WРТ (р )- передаточная функция регулятора тока; Тм – электромеханическая постоянная времени электропривода; Тэ – электромагнитная постоянная времени главной цепи;
КП – коэффициент усиления тиристорного преобразователя; Ту – постоянная времени системы тиристорного преобразователя; КТ – коэффициент передачи обратной связи по току. Постоянная Тµ определяется запаздыванием системы управления, наличием фильтров и т.п. и является некомпенсируемой малой постоянной времени. Структурная схема разомкнутой цепи регулирования тока показана (рис. 1.21(б)). В этой схеме опущена обратная связь по э.д.с. (Едв).
Так как вносимая ею ошибка по модулю и фазе не большая. В общем виде передаточная функция разомкнутого контура равна:
 (1.42)
(1.42)
откуда
 (1.43)
(1.43)
После компенсации большой постоянной времени передаточная функция разомкнутого контура приводиться к виду:
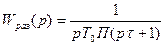 ,
,
где Т0 – постоянная, которая определяется из условия максимальной частоты пропускания замкнутого контура.
При 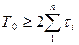 уравнение можно записать
уравнение можно записать
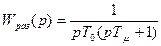 ; (1.45)
; (1.45)
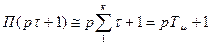 ; (1.46)
; (1.46)
где 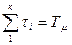 - сумма малых постоянных времени.
- сумма малых постоянных времени.
Передаточная функция объекта регулирования с учетем равенства запишется:
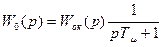 (1.47)
(1.47)
Подставив в уравнение (7.7.4) уравнение (7.7.6) и (7.7.8) будем иметь, с учетом условия оптимизации T0=2Тm,
 (1.48)
(1.48)
Для контура тока рис(12.б)
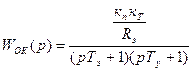 (1.49)
(1.49)
Подставим (1.49) в (1.48)
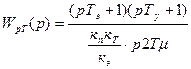 (1.50)
(1.50)
Этой передаточной функции соответствует пропорциональный интегрально – дифференциальный регулятор (ПИД). Если предположить, что система управления безинерционна (Тy=0), то:
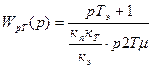 (1.51)
(1.51)
Постоянная времени интегрирования регулятора тока
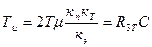 (1.52)
(1.52)

(а)
(б)
Рис. 1.21 Структурная схема токового контура.
Постоянная времени обратной связи регулятора тока:
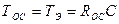 (1.53)
(1.53)
Передаточный коэффициент обратной связи по току:
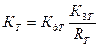 (1.54)
(1.54)
где КдТ – передаточный коэффициент датчика тока, [B/A].
Из уравнений имеем:
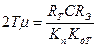 (1.55)
(1.55)
Уравнения позволяют найти параметры регулятора тока.
Структурные схемы оптимизированного контура тока с регулятором приведены на (рис.1.22а,б,в). Передаточная функция замкнутого контура тока имеет вид:
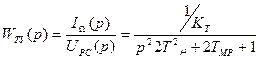 (1.56)
(1.56)
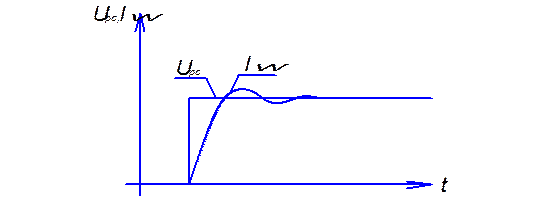
Переходный процесс в контуре тока при внезапном стопорении двигателя эквивалентен скачкообразному приложению возмущения DЕn (рис.1.22), при DUзТ=0 уравнение для тока в замкнутом контуре будет иметь вид:
 (1.57)
(1.57)
где 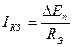
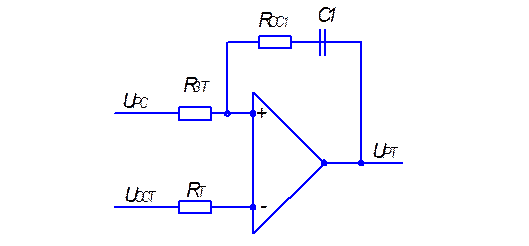
(а)
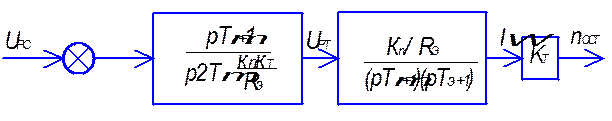
(б)
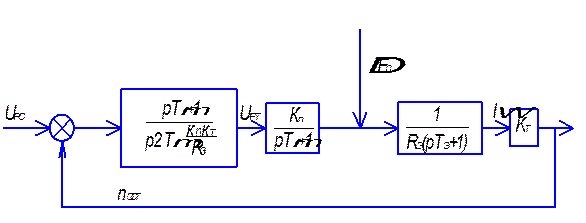
(в)
 (г)
(г)
Рис.1.22 Синтез токового контура.
Поведение тока (рис.1.23 г) под действием скачка напряжения DUЗТ (при DЕn=0) описывается уравнением:
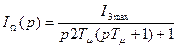 ,(1.58)
,(1.58)
где 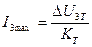 .
.
После оптимизации контура тока оптимизируют контур скорости. Структурная схема разомкнутого контура скорости, после отбрасывания члена второго порядка в уравнении , приведена на рис.1.23а.
Для получения астатических характеристик по входному и возмущающему воздействиях регулятор скорости выбирается пропорционально – интегральным (ПИ) с передаточной функцией. Оптимизация ведется по симметричному критерию.
 (1.59),
(1.59),
где  ;
; 
Эквивалентная постоянная интегрирования контура скорости вращения:
 (1.60)
(1.60)
Эквивалентная малая постоянная времени контура частоты вращения равна:
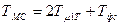 (1.61)
(1.61)

(а)

(б)
(в)
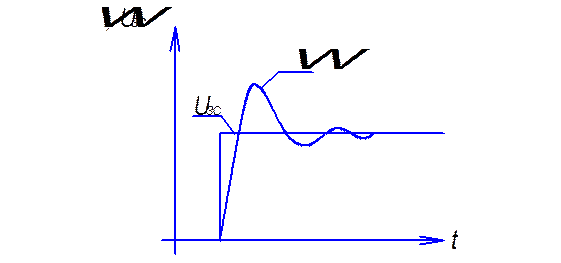
Рис.1.23 Синтез скоростного контура.
Передаточная функция замкнутой системы регулирования имеет вид:
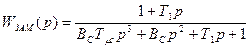 (1.62)
(1.62)
Частота среза системы выбирается из условия максимального знака по фазе:
 (1.63)
(1.63)
На рис.1.23в приведен характер изменения скорости при ступенчатом входном воздействии UЗС.
Дата добавления: 2015-06-17; просмотров: 3178;
