DC Motor Characteristic Curves and Speed Regulation

The operating characteristics of a dc motor determine its perfor­mance and represent the relations of the speed n, torque T_e, con­sumption current I, power input Р₁, and efficiency to the power out­put P₂. These relations correspond to the natural operating condi­tions, with the motor held uncontrollable and the supply voltage constant. If the shaft output P₂ changes, the armature current chan­ges too, for which reason the characteristic curves are often taken as the plots of the motor parameters versus armature current. The torque and speed of a shunt motor plotted against the armature cur­rent appear in Fig. 8.16b.

The rotational speed of the motor is given by the expression n = (V - IR_а)/сФ.

An increase in the load on the motor shaft leads to an increased armature current, which adds to the voltage drop IR_a across the armature resistance and brush contacts. Because the machine re­mains uncontrollable, the field current and, hence, the magnetic flux remain constant. But with an increase in the armature current, the demagnetizing effect of the armature reaction makes itself felt stronger and the flux Ф becomes slightly weaker. As IR_a increases, the speed falls, but a decrease in Ф causes the speed to grow. The voltage drop usually affects the speed to a greater extent than the-armature reaction, so that the speed decreases with increasing arma­ture current. The change in speed from full load to no load for this type of motor is a small percentage of the full-load speed and does not exceed 5% of the rated value. Shunt motors thus exhibit a flat speed characteristic.

The torque of the motor is T_e = КIФ. With the flux kept invariable, the plot of torque as a function of armature current can essentially assume the form of a straight line. However, with more and more load thrown in, armature reaction comes into play and brings about a slight reduction of flux, so the torque-current curve deflects downward from the straight line.

The wiring diagram of the star­ter for a series wound motor appears in Fig. 8.17a. The motor starter has only two terminals because the field winding and the armature winding form one series circuit. Fig. 8.17b illustrates the perfor­mance characteristics of this motor. The speed of a series motor is defined by the expression

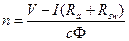
where R_sw is the resistance of the series field winding.

In a series motor the flux does not remain constant but sharply varies with load, causing substantial changes in speed. Since the voltage drop in the resistances of the armature and field windings-is very small in comparison with the impressed voltage, the speed may be given by an approximate expression n = V/сФ.

Neglecting the iron saturation, the flux can be taken to be pro­portional to the field current which is equal to the armature cur­rent. So, in the series motor the speed varies inversely with the armature current and falls quite rapidly as its load grows. In other words, the series motor exhibits a drooping speed characteristic. At lighter loads the motor runs at higher speed. At no load, when I = 0, the speed rapidly grows high beyond safe limits. The motor is said to be racing at overspeed.

Thus, it is impermissible to run a series motor without load or at too light loads. The minimum load must not be less than 25% to 30% of the rated load. At the load below the minimum safe limit, the motor rapidly gains speed to a runaway value and its armature may break down. That is why, where loads are likely to be thrown out or sharply decreased, the use of a series motor is impractical. In motors delivering very small powers, the load throw-off does not •cause runaway since the mechanical losses prove a sufficient load on such motors.

Considering that the air-gap flux is proportional to the armature current, Ф = c'I, the expression for the torque of a series motor can be written as T_e — КIФ = K'I², where K' = Kc', i.e. the torque is proportional to the square of current. But at large currents, the increasing field saturates the magnetic circuit and the torque-cur­rent curve approaches the straight line. Series motors thus develop high torques at low speed and low torques at high speed. This featu­re makes this type of motor very attractive for use in transportation and hoisting facilities.

Compound motors can be of both the cumulative compound and differential compound types. Differentially-wound motors have not received recognition because they display poor starting characteristics and operate unsteadily. The properties of compound motors fall between those of series and shunt motors.

Any dc motor lends itself to smooth and efficient speed control over a wide range. This important feature makes dc motors rather popular and often indispensable in some fields of application.

Whatever the circuit of its excitation, the motor runs at a speed •definable by the expression: n = [V – I(R_a –R_sw)]/cФ, where R_sw is the series winding resistance, which is equal to zero for a shunt motor. This expression reveals that the motor speed depends on the impressed voltage, armature circuit resistance, and magnetic flux.

Speed control by adjusting the impressed voltage is suitable where the motor receives power from a separate voltage source such as a generator.

Speed control by adjusting the value of R_a relies on an adjustable-rheostat in series with the armature. In distinction from the star­ting rheostat (motor starter), this resistor is designed to stand up to currents for a long time. Since a large amount of power is lost in the adjustable resistor, the efficiency of the motor with resistance control is low. That is why, the resistance method of speed control finds rare uses.

Speed control by adjusting the air-gap flux, namely, the field current, is the most popular as well as the most economical method of control. In shunt and compound motors, an adjustable rheostat is used to control the field current. In series motors, an adjustable resistor connected across the field circuit provides for speed con­trol.