Human Curves

Melodic contours are, in the sights of this movement theory of music, about the sequence of movement directions of a fictional mover. When the melody’s pitch changes, the music is narrating to your auditory system that the depicted mover is changing his or her direction of movement. If this really is what melody means, then melody and people should have similar turning behavior.

How quickly do people turn when moving? Get on up and let’s see. Walk around and make a turn or two. Notice that when you turn 90 degrees, you don’t usually take 10 steps to do so, and you also don’t typically turn on a dime. In order to get a better idea of how quickly people tend to change direction, I set out to find videos of people moving and changing direction. After some thought, undergraduate RPI student Eric Jordan and I eventually settled on videos of soccer players. Soccer was perfect because players commonly alter their direction of movement as the ball’s location on the field rapidly changes. Soccer players also exhibit the full range of human speeds, allowing us to check whether turning rate depends on speed. Eric measured 126 instances of approximately right‑angle turns, and in each case, recorded the number of steps the player took to make the turn. Figure 29 shows the distribution for the number of steps taken. As can be seen in the figure, these soccer players typically took two steps to turn 90 degrees, and this was the case whether they were walking, jogging, or running. Casual observation of movers outside of soccer games–such as in coffee shops–suggests that this is not a result peculiar to soccer.

If music sounds like human movers, then it should be the case that the depicted mover in music turns at rates typical for humans. Specifically, then, we expect the musical mover to take a right‑angle turn in about two steps on average. What does this mean musically? A step in music is a beat, and so the expectation is that music will turn 90 degrees in about two beats. But what does it mean to “turn 90 degrees” in music?

Recall that the maximum pitch in a song means the mover is headed directly toward the listener, and the lowest pitch means the mover is headed directly away. That is a 180‑degree difference in mover direction. Therefore, when a melody moves over the entirety of the tessitura (the melody’s pitch range), it means that the depicted mover is changing direction by 180 degrees (either from toward you to away from you, or vice versa). And if the melody spans just the top or bottom half of the tessitura, it means the mover has turned 90 degrees. Because human movers take about two steps to turn 90 degrees–as we just saw–we expect that melodies tend to take about two beats to cross the upper or lower half of the tessitura.

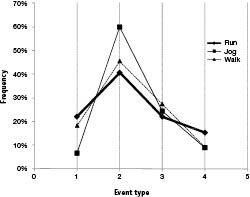
Figure 29 . Distribution of the number of footsteps soccer players take to turn 90 degrees, for walkers, joggers, and runners. The average number of footsteps for a right‑angle turn for walkers is 2.16 (SE 0.17, n=22); for joggers, 2.21 (SE 0.11, n=45); and for runners, 2.23 (SE 0.13, n=59).

To test this, we measured from the Dictionary of Musical Themes melodic “runs” (i.e., strictly rising or strictly falling sequences of notes) having at least three notes within the upper or lower half of the tessitura (and filling at least 80 percent of the width of that half tessitura). These are among the clearest potential candidates for 90‑degree turns in music. Figure 30 shows how many beats music typically takes to do its 90‑degree turns. The peak is at two beats, consistent with the two footsteps of people making 90‑degree turns while moving. Music turns as quickly as people do!

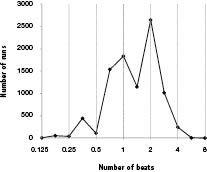
Figure 30 . Distribution of the number of beats for a theme “run” to cover the top or bottom half of the tessitura. The most common number of beats to cross half the tessitura is two, consistent with how quickly people turn 90 degrees. (Runs had three or more notes moving in the same direction, and all within the top or bottom half of the tessitura, and filling at least 80% of its half tessitura.)

This close fit between human and melodic turning rates is, as we will see, helpful in trying to understand regularities in the overall structure of melody, which we delve into next.