Where’s the Moving Pitch?

Throughout this chapter thus far, I have been suggesting that the Doppler effect is the ecological foundation of melody. One potential stumbling block for this hypothesis that I have until now avoided mentioning is that we’re not generally aware of these Doppler shifts in pitch. We may sometimes consciously notice them coming from skateboards, bikes, cars, and trains, but do we notice them coming from moving people ? If our auditory system is listening to the Doppler shifts of people, then wouldn’t we have noticed? Not necessarily. As we discussed in Chapter 1, in the section titled “Under the Radar,” your conscious self not only doesn’t acknowledge these lower‑level stimuli; it typically does not even have access to them. Just as your conscious self sees objects, not visual contour junctions, your conscious self hears the behaviors and actions of movers, not the auditory substrate out of which the whole is built. Your conscious self tends to latch onto the invariants out there–a pink room with a variety of colored lights will have a variety of spectra, but you’ll typically see the walls as uniformly pink. Similarly, when a mover in your midst is making sounds, your conscious self will focus on invariants such as what the mover is doing. Your auditory system will hear all of the lower‑level structure, including the (detectable) pitch modulations due to the Doppler effect, but all that will tend to stay below the radar because you don’t need to know the details.

It would not, then, be surprising if our auditory system detects (and uses) Doppler shifts from human movers and yet we don’t consciously notice it. But one might wonder whether our auditory system can possibly detect Doppler shifts for movers going human speeds in the first place. If I am walking at one meter per second, then the difference in pitch between the highest and lowest pitch in the Doppler range is small, roughly about a tenth of a semitone on the piano. The fastest sprints possible by humans are about 10 meters per second, and even at these speeds the Doppler pitch range is only about a single semitone on the piano (e.g., from C to C#). Thus, whereas the Doppler pitch modulations for trains, planes, and automobiles are sizable because those vehicles move quickly, the pitch modulations for humans are small. Tiny as these Doppler pitch shifts may be, however, our auditory system is exquisitely sensitive to pitch changes, capable of detecting differences as small as about 0.3 percent of the frequency, or about 5 percent of a semitone–sensitive enough to distinguish even the pitch shifts of walkers.

So our ears are sensitive enough. But if one thinks more carefully about how our feet make sounds, there appears to be a big problem with the suggestion that the sounds of human movers make Doppler shifts at all. The biggest bang your body makes in motion is when your foot takes a step. But notice that when you are walking and your foot hits the ground, it is moving neither forward nor backward relative to the ground. Your feet are stationary when they touch the ground. But if your sound‑making foot is not moving forward when it makes its sound, then its pitch will not get Doppler shifted upward. That is, even though you are moving steadily forward, your feet are standing still at the moments when they are making their footstep sounds, and so your footstep sounds undergo no Doppler shift. (See Figure 36a.) (This is not a problem that applies to between‑the‑steps gangly bangings, which do Doppler shift.)

Footsteps are, however, more subtle than a simple vertical thud on the ground, and there are multiple avenues in which Doppler shifts may occur. First, even if your footsteps stomp the ground without any forward speed, your body is still moving forward. When the footstep sound waves rise into the air, your big old body bumps into them and reflects them. The waves that your front runs into get reflected forward and are consequently Doppler upshifted, and the waves that reflect off your back get Doppler downshifted, as illustrated in Figure 36b (i). Second, footsteps aren’t the simple vertical ground bangers that Figure 36a would have us believe. For one thing, the dynamics of a footstep are complicated by the fact that the ground is often complicated. Throughout most of our evolutionary history the ground was not smooth as it is today, but covered in grass, brush, and pebbles. When your foot goes in for a landing, it has some forward velocity, and will undergo a sequence of microcollisions with the ground material. This sequence of collisions is a forward‑moving sequence, and will sound higher in pitch (or compressed) to a listener toward whom the mover is directed. (See Figure 36b [ii].) Not only is the ground more complicated than the “stomping” in Figure 36a indicates, but the foot dynamics even on smooth ground are more subtle than I have let on. Our heel hits first, and the contact points move forward along the foot toward the toes (see Figure 36b [iii]). Whether on smooth ground or natural terrain, this sequence of microhits underlying a single step is moving in the direction of the mover, and thus will Doppler shift.

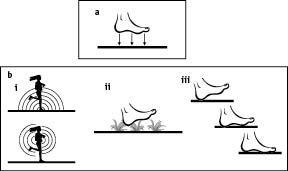
Figure 36 . (a) When a foot hits the ground, it is not moving forward or backward, and therefore has no Doppler shift. But as we’ll discuss, there’s more to the story. (b) (i) Top: The footstep leads to sound waves going in all directions, all at the same frequency (indicated by the spacing between the wave fronts). Bottom: These waves hit the body and reflect off it. Because the mover is moving forward, the sound waves reflected forward will be Doppler shifted to a higher pitch; the waves hitting the mover’s rear will reflect at a lower pitch. (ii) When feet land they don’t simply move vertically downward for a thud. The surface of the ground very often has complex material on it, which the landing foot strikes as it is still moving forward. These complex sounds will have Doppler shifts. (iii) If our feet were like a pirate’s peg leg, then the single thud it makes when hitting the ground would have no Doppler shift. But our feet aren’t peg legs. Instead, our foot lands on its heel, and the point of contact tends to move forward along the bottom of the foot.

Footsteps can, then, Doppler shift, and these shifts are detectable. There is now a third difficulty that can be raised: if Doppler shifts for human movers are fairly meager, then why doesn’t musical melody have meager tessitura width (i.e., meager pitch range for the melody)? The actual tessitura in melody tends to be wider than that achievable by a human mover, corresponding to speeds faster than humans can achieve. Why, if melodic pitch contours are about Doppler pitches, would music exaggerate the speed of the depicted observer? Perhaps for the same reason that exaggeration is commonplace in other art forms. Facial expressions in cartoons, for example, tend to be hyperexaggerations of human facial expressions. Presumably such exaggerations serve as superstimuli, hyperactivating our brain’s mechanisms for detecting the characteristic (e.g., smile or speed), and something about this hyperactivation feels good to us (perhaps a bit like being on a roller coaster).

One final thought concerning the mismatch between the Doppler pitch range and the tessitura widths found in music: could I have been underestimating the size of the Doppler shifts humans are capable of? Although we may only move in the one‑ to ten‑meters‑per‑second range, and our limbs may swing forward at a little more than twice our body’s speed, parts of us may be moving at faster speeds. Recall that your feet hit the ground from heel to toe. The sequence of microhits travels forward along the bottoms of your feet, and the entirety of sound the sequence makes will be Doppler shifted. An interesting characteristic of this kind of sound is that it can act like a sound‑making object that is moving much faster than the object that actually generates it. As an example, when you close scissors, the actual objects–the two blades–are simply moving toward each other. But the point of contact between the blades moves outward along the blades. The sound of closing scissors is a sound whose principal source location is moving, even though no object is actually moving in that manner. This kind of faux‑moving sound maker can go very fast. If two flattish surfaces hit each other with one end just ever so slightly ahead of the other, then the speed of the faux mover can be huge. For example, if you drop a yardstick so as to make it land flat, and one end hits the ground one millisecond before the other end, then the faux mover will have traveled between the yardstick and the ground from one end to the other at about one kilometer per second, or about two thousand miles per hour! The faux mover beneath our stepping feet may, in principle, be moving much faster than we are, and any scissor‑like sound it makes will thus acquire a Doppler pitch range much wider than that due to our body’s natural speed.

Human movers do make sounds that Doppler shift, and these shifts are detectable by our auditory system. And their exaggeration in music is sensible in light of the common role of exaggeration in artistic forms. Melodic contour, we have seen thus far, has many of the signature properties expected of Doppler shifts, lending credence to the idea that the role of melodic pitch contours is to tell the story of the sequence of directions in which a mover is headed. That’s a fundamental part of the kinematic information music imparts about the fictional mover. But that’s only half the story of “kinemusic.” It doesn’t tell us how far away the mover is, something more explicitly spatial. That is the role of loudness, the topic of the rest of this chapter.