Slow Loudness, Fast Pitch

Have you ever wondered why our musical notation system is as it is? In particular, why does our Western music notation system indicate pitch by shifting the notes up and down on the staff, while it indicates loudness symbolically by letters (e.g., pp , f ) along the bottom? Figure 37 shows a typical piece of music. Even if you don’t read music–and thus don’t know exactly which pitch each note is on–you can instantly interpret how the pitch varies in the melody. In this piece of music, pitch rises, wiggles, falls, falls, falls yet again, only to rise and tumble down. You can see what pitch does because the notation system creates what is roughly a plot of pitch versus time. Loudness, on the other hand, must be read off the letters along the bottom, and their meaning unpacked from your mental dictionary: p for “quiet,” f for “loud,” and so on. Why does pitch get a nice mapping onto spatial position, whereas loudness only gets a lookup table, or glossary?

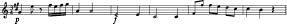
Figure 37 . The usual notation, where vertical position indicates pitch, and intensities are shown along the bottom. The music is a simplification of the seventh through twelfth measures from Johann Christoph Friedrich Bach’s Menuet and Alternativo . It utilizes standard music notation. Standard notation is sensible because pitches vary much more quickly than loudness, so it tends not to be a problem to have to read the loudness levels along the bottom.

Music notation didn’t have to be like this. It could do the reverse: give loudness the spatial metaphor, and relegate pitch to being read along the bottom in symbols. Figure 38 shows the same excerpt we just saw in Figure 37, but now in this alternative musical notation system. Going from the lowest horizontal line upward, the lines now mean pianissimo (pp ), piano (p ), mezzo forte (mf ), forte (f ), and fortissimo (ff ). The pitches for each note of the song are now shown along the bottom. Once one sees this alternative notation system in Figure 38, it becomes obvious why it is a terrible idea. When vertical height represents loudness, vertical height tends to just stay constant for long periods of time. The first eight notes are all at one loudness level (piano ), and the remaining 12 are all at a second loudness level (forte ). Visually there are just two plateaus, severely underutilizing your visual talents for seeing spatial wiggles. In standard notation, where pitch is spatially represented, on the other hand, the notes vary vertically much more on the page. Not only does our hypothetical alternative notation underutilize the capabilities of the visuospatial code, it overutilizes the letter codes. We end up with “word salad” along the bottom. In this case, there are 15 instances where the pitch had to be written down, nearly as many as there are notes in the excerpt. In standard notation, where loudness is coded via letters, there were just two letters along the bottom (see Figure 37 again).

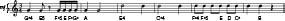
Figure 38 . A notation system in which vertical position indicates intensity, and pitches are shown along the bottom. This is the same excerpt from J.C.F. Bach as in Figure 37 but here the notation schemes for pitch and loudness have been swapped. This is not a good way to notate music because most of the note‑to‑note modulations are in pitch, not in loudness, which means an overabundance of pitch labels along the bottom, and little use of the vertical dimension within the horizontal bars. (To read the pitches along the bottom, “E5,” for example, is the E pitch at the fifth octave. When the octave is not labeled, it is presumed to be that of the last mentioned octave.)

The reason this alternative music notation system is so bad is, in one sense, obvious. In music, pitch typically varies quickly, often from note to note. Loudness, on the other hand, is much less variable over time. As exemplified by the excerpt in Figure 37, pitch can change at very short time scales, such as a 16th or 32nd note, but intensities typically persist for many measures before they change. To illustrate this, consider the fictional piece of music shown in Figure 39 (using standard music notation). In this example, pitch hardly ever changes, and loudness is changing very quickly. Music is never like this, which is why the standard notation system is a good one. The standard music notation system is so useful for music because it gives the quickly varying musical quality–pitch–the spatial metaphor, and relegates to the glossary the musical quality that stays much more constant: loudness.

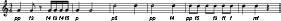
Figure 39 . An alternative kind of music that never happens (shown in regular notation). If music were often like this, then the alternative notation system in Figure 38 would be sensible. (This fictional music was created by taking J.C.F. Bach’s piece in Figure 38, keeping the notes as in that reverse notation system, but then pretending they represent pitches, as in normal notation (“f4” means “ffff ”).

To get a more quantitative measure of how quickly pitches and loudnesses change over time, Sean Barnett measured the distribution of time spent on a pitch before changing (Figure 19, earlier), and Eric Jordan measured the distribution of time spent at a given level of loudness before changing (Figure 40 below). One can see that pitches typically switch after about half a beat to a beat, whereas intensities change after about 10 beats.

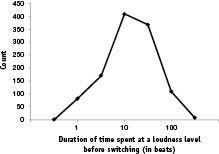
Figure 40. Distribution of time spent at a loudness level before switching. One can see that loudness durations tend to be about 10 beats, and very often as long as 30 or more beats. This is more than an order of magnitude greater than the time scales for durations at the same pitch, which tend to be about a half a beat to a beat. These data were measured from Denes Agay’s An Anthology of Piano Music, Vol. II: The Classical Period .

While it is obvious why the standard notation system is smarter than my hypothetical “reverse” one for music, it is not obvious why music is like this in the first place. Why does music have “fast pitches” and “slow loudnesses”? If music sounds like movement, and loudness modulations are selected to sound like those due to spatial proximity, then the answer is straightforward. In order to significantly change loudness, the mover must move some distance through space. Melodic pitch, on the other hand, is about directedness toward the listener. In contrast to movement through space, which takes a relatively long time, a mover can “turn on a dime.” In a single step, a mover can turn about 45 degrees with ease (and typically does), which would translate to a fourth of the tessitura width (on average). Melodic pitch changes more quickly than loudness in music simply because human movers can change direction more quickly than they can change their proximity to the listener. That’s why music never sounds like the fictional piece of music in Figure 39, and that’s why our Western musical notation system is an efficient one. The comparative time scales of loudness and melodic pitch are what we should expect if music sounds like human movers, with loudness modulated by the spatial proximity and melodic pitch by the direction of the depicted mover.

In addition to the time scale for loudness modulations being consistent with that for changes in proximity, additional evidence for proximity as the meaning of loudness is provided in four Encore sections:

Encore 4: “Distant Beat” I will discuss how the nearer movers are, the more of their gait sounds are audible, and how this is also found in music: louder portions of music tend to have more notes per beat. (This was also mentioned earlier in this chapter as we finished up our discussion of rhythm, because it concerns the interaction between rhythm and loudness.)

Encore 6: “Fast Tempo, Wide Pitch” I discuss how, as expected from theory, music with a faster tempo has a wider pitch range for its melody. This Encore section also shows, however, that–as predicted–the range of loudnesses in a piece is not correlated with tempo.

Encore 7: “Newton’s First Law of Motion” This Encore section takes up a variety of predictions related to the inertia of moving objects, on the one hand, and the asymmetry between pitch rises and pitch falls, on the other. We will predict, and data will confirm, that this asymmetry changes as a function of loudness: when music indicates (by high loudness level) that the mover is close, the probability rises of long pitch runs downward.

Encore 8: “Medium Encounters” This Encore section concerns regularities in how movers distribute themselves in distance from a listener, and makes predictions about how frequently music makes use of various loudness levels.